题目内容
10.若实数x,y满足约束条件$\left\{\begin{array}{l}{2x+y-4≤0}\\{x-2y-2≤0}\\{x-1≥0}\end{array}\right.$,则3x-y的最大值为6.分析 作出可行域,变形目标函数,平移直线y=2x可得结论.
解答  解:作出约束条件$\left\{\begin{array}{l}{2x+y-4≤0}\\{x-2y-2≤0}\\{x-1≥0}\end{array}\right.$,所对应的可行域如图,
解:作出约束条件$\left\{\begin{array}{l}{2x+y-4≤0}\\{x-2y-2≤0}\\{x-1≥0}\end{array}\right.$,所对应的可行域如图,
变形目标函数可得y=3x-z,平移直线y=3x可知当直线经过点A(2,0)时,
直线的截距最小,z取最大值,代值计算可得z=3x-y的最大值为6,
故答案为:6
点评 本题考查简单线性规划,准确作图是解决问题的关键,属中档题.

练习册系列答案
相关题目
20.设函数f(x)=$\left\{\begin{array}{l}{(x-a)^2}+e,x≤2\\ \frac{x}{1nx}+a+10,x>2\end{array}$,(e是自然对数的底数),若f(2)是函数f(x)的最小值,则a的取值范围是( )
| A. | [-1,6] | B. | [1,4] | C. | [2,4] | D. | [2,6] |
1.已知函数$f(x)=\left\{{\begin{array}{l}{{2^x}-1,x≤1}\\{1+{{log}_2}x,x>1}\end{array}}\right.$,则函数f(x)的零点是( )
| A. | x=0或$x=\frac{1}{2}$ | B. | x=-2或x=0 | C. | $x=\frac{1}{2}$ | D. | x=0 |
5.执行如图所示的程序框图,如果输出的结果为0,那么输入的x为( )


| A. | $\frac{1}{9}$ | B. | -1或1 | C. | -l | D. | l |
15.若${(a+i)^2}-\frac{1}{i}∈R(a∈R,i$是虚数单位),则a=( )
| A. | 1 | B. | 0 | C. | 一$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
12.在△ABC中,tanC=2,BC边上的高为AD,D为垂足,且BD=2DC,则cosA=( )
| A. | $\frac{3}{10}$ | B. | $\frac{\sqrt{10}}{10}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{3\sqrt{10}}{10}$ |
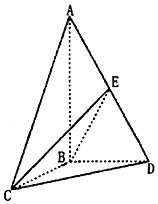 如图,三棱锥A-BCD中,AB⊥平面BCD,AC=AD=2,BC=BD=1,点E是线段AD的中点.
如图,三棱锥A-BCD中,AB⊥平面BCD,AC=AD=2,BC=BD=1,点E是线段AD的中点.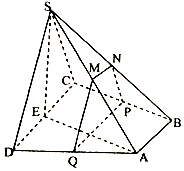 如图,四棱锥S-ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=SD=CD=AD=2AB,M,N分别为SA,SB的中点,E为CD中点,过M,N作平面MNPQ分别与BC,AD交于点P,Q,若$\overrightarrow{DQ}$=t$\overrightarrow{DA}$.
如图,四棱锥S-ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=SD=CD=AD=2AB,M,N分别为SA,SB的中点,E为CD中点,过M,N作平面MNPQ分别与BC,AD交于点P,Q,若$\overrightarrow{DQ}$=t$\overrightarrow{DA}$.