题目内容
9.平面内定点财(1,0),定直线l:x=4,P为平面内动点,作PQ丄l,垂足为Q,且$|\overrightarrow{PQ}|=2|\overrightarrow{PM}|$.(I)求动点P的轨迹方程;
(II )过点M与坐标轴不垂直的直线,交动点P的轨迹于点A、B,线段AB的垂直平分 线交x轴于点H,试判断$\frac{|HM|}{|AB|}$-是否为定值.
分析 (Ⅰ)设P(x,y),由题意可得Q(4,y),又M(1,0),结合且$|\overrightarrow{PQ}|=2|\overrightarrow{PM}|$.即可求得点P的轨迹方程;
(Ⅱ)设过点M的直线斜率存在时的方程为y=k(x-1),A(x1,y1),B(x2,y2),AB方程代入$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$得(3+4k2)x2-8k2x+4k2-12=0.
利用韦达定理,可求AB的中点D(x0,y0),令y=0可得H坐标,利用弦长公式求出|HM|、|AB|即可.
解答 :(1)设P(x,y),则由已知得Q(4,y),又M(1,0),
∴$\overrightarrow{PQ}$=(4-x,0),$\overrightarrow{PM}$=(1-x,-y),
∵$|\overrightarrow{PQ}|=2|\overrightarrow{PM}|$.∴4[(1-x)2+y2]=(4-x)2,
整理得$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.
(Ⅱ)依题意直线AB的斜率垂直且不为0,可设AB:y=k(x-1)(k≠0),
A(x1,y1),B(x2,y2)
代入$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$得(3+4k2)x2-8k2x+4k2-12=0.
∴x1+x2=$\frac{8{k}^{2}}{3+4{k}^{2}}$,x1x2=$\frac{4{k}^{2}-12}{3+4{k}^{2}}$,
设AB的中点为D(x0,y0),
${x}_{0}=\frac{4{k}^{2}}{3+4{k}^{2}},{y}_{0}=k({x}_{0}-1)=\frac{-3k}{3+4{k}^{2}}$,
线段AB的垂直平分线为:y-$\frac{-3k}{3+4{k}^{2}}=-\frac{1}{k}(x-\frac{4{k}^{2}}{3+4{k}^{2}})$,令y=0,${x}_{H}=\frac{{k}^{2}}{3+4{k}^{2}}$,
∴|HM|=|1-$\frac{{k}^{2}}{3+4{k}^{2}}$|=$\frac{3(1+{k}^{2})}{3+4{k}^{2}}$,
|AB|=$\sqrt{1+{k}^{2}}$|x1-x2|=$\frac{12(1+{k}^{2})}{3+4{k}^{2}}$
断$\frac{|HM|}{|AB|}$=$\frac{1}{4}$(定值).
点评 本题考查了动点P的轨迹方程、椭圆的标准方程与简单性质和直线与圆位置关系,弦长公式等知识,突出方程思想,转化思想的考查与运用,属于中档题.

| A. | [-1,6] | B. | [1,4] | C. | [2,4] | D. | [2,6] |
| A. | y=f(x)是偶函数,在$(0,\frac{π}{2})$上单调递增 | B. | y=f(x)是奇函数,在$(0,\frac{π}{4})$上单调递增 | ||
| C. | y=f(x)是偶函数,在$(0,\frac{π}{2})$上单调递减 | D. | y=f(x)是奇函数,在$(0,\frac{π}{4})$上单调递减 |
| A. | x=0或$x=\frac{1}{2}$ | B. | x=-2或x=0 | C. | $x=\frac{1}{2}$ | D. | x=0 |
| A. | $\frac{3}{10}$ | B. | $\frac{\sqrt{10}}{10}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{3\sqrt{10}}{10}$ |
 在△ABC中,角A、B、C所对的边分别是a、b、c,已知$\sqrt{3}a=2csinA$且c<b.
在△ABC中,角A、B、C所对的边分别是a、b、c,已知$\sqrt{3}a=2csinA$且c<b. 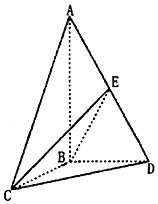 如图,三棱锥A-BCD中,AB⊥平面BCD,AC=AD=2,BC=BD=1,点E是线段AD的中点.
如图,三棱锥A-BCD中,AB⊥平面BCD,AC=AD=2,BC=BD=1,点E是线段AD的中点.