题目内容
18.已知球的直径为4,则该球的表面积积为16π.分析 直接利用球的表面积公式求解即可.
解答 解:球的直径为4,球的半径为:2,
球的表面积为:4π×22=16π.
故答案为:16π.
点评 本题考查球的表面积的求法,是基础题.

练习册系列答案
相关题目
8.复数z=1-2i,$\overline{z}$是z的共轭复数,则复平面内复数z•$\overline{z}$-i对应的点所在象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.角α的终边经过点P(b,4),且cosα=-$\frac{3}{5}$,则b的值为( )
| A. | ±3 | B. | 3 | C. | -3 | D. | 5 |
7.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$与抛物线y2=8x有一个公共的焦点F,且两曲线的一个交点为P,若|PF|=4,则双曲线的离心率为( )
| A. | $\sqrt{2}+1$ | B. | $2({\sqrt{2}+1})$ | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
8.已知f(x)=x4,g(x)=($\frac{1}{3}$)x-λ,若对任意的x1∈[-1,2],存在x2∈[-1,2],使f(x1)≥g(x2)成立,则实数λ的取值范围是( )
| A. | λ≥$\frac{1}{9}$ | B. | λ≥2 | C. | λ≥-$\frac{8}{9}$ | D. | λ≥-13 |
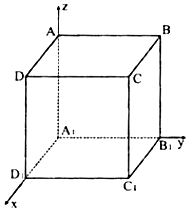 如图建立空间直角坐标系,已知正方体的棱长为2.
如图建立空间直角坐标系,已知正方体的棱长为2.