题目内容
8.已知f(x)=x4,g(x)=($\frac{1}{3}$)x-λ,若对任意的x1∈[-1,2],存在x2∈[-1,2],使f(x1)≥g(x2)成立,则实数λ的取值范围是( )| A. | λ≥$\frac{1}{9}$ | B. | λ≥2 | C. | λ≥-$\frac{8}{9}$ | D. | λ≥-13 |
分析 条件对任意x1∈[-1,2],总存在x2∈[-1,2],使f(x1)≥g(x2)成立等价为上f(x)min≥g(x)min即可.
解答 解:∵x1∈[-1,2],∴0≤f(x1)≤16,
∵x2∈[-1,2],∴$\frac{1}{9}$-λ≤g(x2)≤3-λ,
若对任意x1∈[-1,2],总存在x2∈[-1,2],使f(x1)≥g(x2)成立,
则f(x)min≥g(x)min即可,
即0≥$\frac{1}{9}$-λ,
解得λ≥$\frac{1}{9}$,
故选:A.
点评 本题主要考查函数值的大小比较以及不等式恒成立问题,将条件转化为求函数最值之间的关系是解决本题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
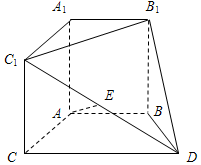 在如图所示的几何体中,A1B1C1-ABC是直三棱柱,四边形ABDC是梯形,AB∥CD,且$AB=BD=\frac{1}{2}CD=2$,∠BDC=60°,E是C1D的中点.
在如图所示的几何体中,A1B1C1-ABC是直三棱柱,四边形ABDC是梯形,AB∥CD,且$AB=BD=\frac{1}{2}CD=2$,∠BDC=60°,E是C1D的中点.