题目内容
10．已知命题p：方程$\frac{x^2}{m+1}+\frac{y^2}{m-1}=1$表示焦点在x轴上的双曲线，命题q：关于x的方程x2+2mx+2m+3=0无实根，（1）若命题p为真命题，求实数m的取值范围；
（2）若“p∧q”为假命题，“p∨q”为真命题，求实数m的取值范围．
分析 （1）若命题p为真命题，则$\left\{\begin{array}{l}m+1＞0\\ m-1＜0\end{array}\right.$，解得实数m的取值范围；
（2）若“p∧q”为假命题，“p∨q”为真命题，则命题p，q一真一假，进而可得实数m的取值范围．
解答 解：（1）∵方程$\frac{x^2}{m+1}+\frac{y^2}{m-1}=1$表示焦点在x轴上的双曲线，
∴$\left\{\begin{array}{l}m+1＞0\\ m-1＜0\end{array}\right.$，
即-1＜m＜1，…（4分）
∴若命题p为真命题，则实数m的取值范围是（-1，1）…（5分）
（2）若“p∧q”为假命题，“p∨q”为真命题，
则p，q为一个真命题，一个假命题，…（7分）
若关于x的方程x2+2mx+2m+3=0无实根，
则判别式△=4m2-4（2m+3）＜0，…（8分）
即m2-2m-3＜0，得-1＜m＜3．…（9分）
若p真q假，则$\left\{\begin{array}{l}-1＜m＜1\\ m≤-1，或m≥3\end{array}\right.$，此时无解，…（10分）
柔p假q真，则$\left\{\begin{array}{l}-1＜m＜3\\ m≤-1，或m≥1\end{array}\right.$，得1≤m＜3，…（11分）
综上，实数m的取值范围是[1，3）…（12分）
点评 本题以命题的真假判断与应用为载体，考查了双曲线的标准方程，方程根的存在性及个数判断，难度中档．
练习册系列答案
相关题目
20．已知命题p：不等式ax2+ax+1＞0的解集为R，则实数a∈（0，4）；命题q“x2-2x-8＞0”是“x＞5”的必要不充分条件，则下列命题正确的是（ ）
| A． | p∧q | B． | p∧（￢q） | C． | （￢p）∧（￢q） | D． | （￢p）∧q |
1．若将函数f（x）=sin2x+cos2x的图象向左平移φ个单位，所得图象关于y轴对称，则φ的最小正值是（ ）
| A． | $\frac{π}{8}$ | B． | $\frac{π}{4}$ | C． | $\frac{3π}{8}$ | D． | $\frac{3π}{4}$ |
如图，在Rt△AOB中，∠OAB=$\frac{π}{6}$，斜边AB=4，D是AB中点，现将Rt△AOB以直角边AO为轴旋转一周得到一个圆锥，点C为圆锥底面圆周上一点，且∠BOC=90°，
2．已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点为F（3，0），过点F的直线交椭圆于A．B两点．若AB的中点坐标为（1，-$\frac{\sqrt{5}}{5}$），则E的方程为（ ）
| A． | $\frac{{x}^{2}}{10}$+y2=1 | B． | $\frac{{x}^{2}}{19}$+$\frac{{y}^{2}}{10}$=1 | C． | $\frac{{x}^{2}}{27}$+$\frac{{y}^{2}}{18}$=1 | D． | $\frac{{x}^{2}}{18}$+$\frac{{y}^{2}}{9}$=1 |
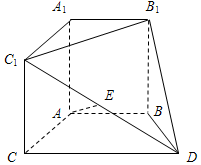在如图所示的几何体中，A1B1C1-ABC是直三棱柱，四边形ABDC是梯形，AB∥CD，且$AB=BD=\frac{1}{2}CD=2$，∠BDC=60°，E是C1D的中点．