题目内容
7.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$与抛物线y2=8x有一个公共的焦点F,且两曲线的一个交点为P,若|PF|=4,则双曲线的离心率为( )| A. | $\sqrt{2}+1$ | B. | $2({\sqrt{2}+1})$ | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
分析 求出抛物线的焦点坐标,然后求解P的坐标,利用焦半径公式求出a,求解双曲线的离心率即可.
解答 解:抛物线y2=8x的焦点F(2,0),两曲线的一个交点为P,
若|PF|=4,则P(2,4)或(2,-4),
可得:$\frac{{b}^{2}}{a}=4$,即:$\frac{4-{a}^{2}}{a}=4$,解得a=2$\sqrt{2}-2$,
解得双曲线的离心率为:$\frac{c}{a}$=$\frac{2}{2\sqrt{2}-2}$=$\sqrt{2}+1$.
故选:A.
点评 本题主要考查了双曲线,抛物线的简单性质.考查了学生综合分析问题和基本的运算能力.解答关键是利用性质列出方程组.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A.B两点.若AB的中点坐标为(1,-$\frac{\sqrt{5}}{5}$),则E的方程为( )
| A. | $\frac{{x}^{2}}{10}$+y2=1 | B. | $\frac{{x}^{2}}{19}$+$\frac{{y}^{2}}{10}$=1 | C. | $\frac{{x}^{2}}{27}$+$\frac{{y}^{2}}{18}$=1 | D. | $\frac{{x}^{2}}{18}$+$\frac{{y}^{2}}{9}$=1 |

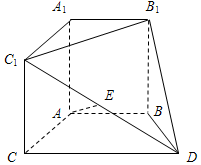 在如图所示的几何体中,A1B1C1-ABC是直三棱柱,四边形ABDC是梯形,AB∥CD,且$AB=BD=\frac{1}{2}CD=2$,∠BDC=60°,E是C1D的中点.
在如图所示的几何体中,A1B1C1-ABC是直三棱柱,四边形ABDC是梯形,AB∥CD,且$AB=BD=\frac{1}{2}CD=2$,∠BDC=60°,E是C1D的中点.