题目内容
6.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长是短轴长的$\sqrt{2}$倍,直线y=-x+1与椭圆C相交于A,B两点,且弦AB的长为$\frac{4\sqrt{5}}{3}$,求此椭圆的方程.分析 由已知可得a2=2b2,化椭圆方程为x2+2y2-2b2=0,联立直线方程与椭圆方程,利用弦长公式列式求得b2,则椭圆方程可求.
解答 解:由题意a2=2b2,
则椭圆方程为$\frac{{x}^{2}}{2{b}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,即x2+2y2-2b2=0
联立$\left\{\begin{array}{l}{y=-x+1}\\{{x}^{2}+2{y}^{2}-2{b}^{2}=0}\end{array}\right.$,得3x2-4x+2-2b2=0.
△=16-12(2-2b2)=24b2-8>0,得${b}^{2}>\frac{1}{3}$.
设A(x1,y1),B(x2,y2),
则${x}_{1}+{x}_{2}=\frac{4}{3},{x}_{1}{x}_{2}=\frac{2-2{b}^{2}}{3}$.
∴$|{{x_1}-{x_2}}|=\frac{{\sqrt{24{b^2}-8}}}{3}$,则$|{AB}|=\frac{{4\sqrt{3{b^2}-1}}}{3}=\frac{{4\sqrt{5}}}{3}$.
解得b2=2.
∴椭圆方程为$\frac{x^2}{4}+\frac{y^2}{2}=1$.
点评 本题考查椭圆的简单性质,考查了直线与椭圆位置关系的应用,训练了弦长公式的应用,属中档题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
14.已知函数f(x)=x3-2x,则f(3)=( )
| A. | 1 | B. | 19 | C. | 21 | D. | 35 |
1.若将函数f(x)=sin2x+cos2x的图象向左平移φ个单位,所得图象关于y轴对称,则φ的最小正值是( )
| A. | $\frac{π}{8}$ | B. | $\frac{π}{4}$ | C. | $\frac{3π}{8}$ | D. | $\frac{3π}{4}$ |
11.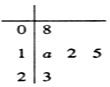 如图是一名篮球运动员在最近5场比赛中所得分数的茎叶图,若该运动员在这5场比赛中的得分的中位数为12,则该运动员这5场比赛得分的平均数不可能为( )
如图是一名篮球运动员在最近5场比赛中所得分数的茎叶图,若该运动员在这5场比赛中的得分的中位数为12,则该运动员这5场比赛得分的平均数不可能为( )
 如图是一名篮球运动员在最近5场比赛中所得分数的茎叶图,若该运动员在这5场比赛中的得分的中位数为12,则该运动员这5场比赛得分的平均数不可能为( )
如图是一名篮球运动员在最近5场比赛中所得分数的茎叶图,若该运动员在这5场比赛中的得分的中位数为12,则该运动员这5场比赛得分的平均数不可能为( )| A. | $\frac{68}{5}$ | B. | $\frac{69}{5}$ | C. | 14 | D. | $\frac{71}{5}$ |
