题目内容
8.我校在高三11月月考中约有1000名理科学生参加考试,数学考试成绩ξ~N(100,a2)(a>0,满分150分),统计结果显示数学考试成绩在80分到120分之间的人数约为总人数的60%,则此次月考中数学成绩不低于120分的学生约有200人.分析 先根据正态分布曲线的图象特征,关注其对称性画出函数的图象,观察图象在80分到120分之间的人数概率,即可得成绩不低于120分的学生人数概率,最后即可求得成绩不低于120分的学生数.
解答 解:∵成绩ξ~N(100,a2),
∴其正态曲线关于直线x=100对称,
又∵成绩在80分到120分之间的人数约为总人数的60%,
由对称性知:成绩在120分以上的人数约为总人数的$\frac{1}{2}(1-0.6)$=0.2,
∴此次数学考试成绩不低于120分的学生约有:0.2×1000=200.
故答案为:200.
点评 本小题主要考查正态分布曲线的特点及曲线所表示的意义等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
8.已知复数z的共轭复数为$\overline{z}$,若(z+2$\overline{z}$)(1-2i)=3-4i(i为虚数单位),则在复平面内,复数z所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
9.设sin(π-θ)=$\frac{1}{3}$,则cos2θ=( )
| A. | $\frac{7}{9}$ | B. | $-\frac{4\sqrt{2}}{9}$ | C. | $-\frac{7}{9}$ | D. | $±\frac{4\sqrt{2}}{9}$ |
13.已知直线x=$\frac{b}{2}$与椭圆C:$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}=1$(a>b>0)交于A、B两点,若椭圆C的两个焦点与A、B两点可以构成一个矩形,则椭圆C的离心率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{10}}{4}$ |
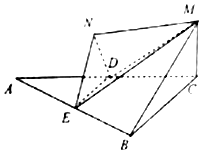 已知如图,△ABC是边长为4的等边三角形,MC⊥平面ABC,D、E分别是线段AC、AB的中点,将△ADE沿DE翻折至△NDE,平面NDE⊥平面ABC.
已知如图,△ABC是边长为4的等边三角形,MC⊥平面ABC,D、E分别是线段AC、AB的中点,将△ADE沿DE翻折至△NDE,平面NDE⊥平面ABC.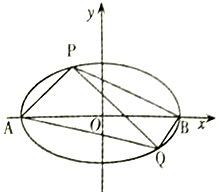 如图,已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,A、B为椭圆的左右顶点,焦点到短轴端点的距离为2,P、Q为椭圆E上异于A、B的两点,且直线BQ的斜率等于直线AP斜率的2倍.
如图,已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,A、B为椭圆的左右顶点,焦点到短轴端点的距离为2,P、Q为椭圆E上异于A、B的两点,且直线BQ的斜率等于直线AP斜率的2倍.