题目内容
17.为便民惠民,某通信运营商推出“优惠卡活动”.其内容如下:卡号的前7位是固定的,后四位从“0000”到“9999”共10000个号码参与该活动,凡卡号后四位带有“6”或“8”的一律作为优惠卡,则“优惠卡”的个数是( )| A. | 1980 | B. | 4096 | C. | 5904 | D. | 8020 |
分析 根据题意,用间接法分析,先计算卡号后四位不带有“6”或“8”的卡的数目,用总数减去其数目即可得答案.
解答 解:根据题意,卡号后四位不带有“6”或“8”的卡,
即只有其余的8个数字的卡有8×8×8×8=84=4096个,
而卡的总数为10000个,
则“优惠卡”有10000-4096=5904个;
故选:C.
点评 本题考查排列、组合的实际应用,注意利用间接法分析,可以避免分类讨论.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
17.已知集合A=$\{1,2,3,4\},B=\{y|y=\sqrt{x},x∈A\}$,则A∩B=( )
| A. | {1} | B. | {1,2} | C. | {1,4} | D. | {1,2,3,4} |
2.定义“函数y=f(x)是D上的a级类周期函数”如下:函数y=f(x),x∈D,对于给定的非零常数a,总存在非零常数T,使得定义域D内的任意实数x都有af(x)=f(x+T)恒成立,此时T为f(x)的周期.若y=f(x)是[1,+∞)上的a级类周期函数,且T=1,当x∈[1,2)时,f(x)=2x(2x+1),且y=f(x)是[1,+∞)上的单调递增函数,则实数a的取值范围为( )
| A. | $[{\frac{5}{6},+∞})$ | B. | [2,+∞) | C. | $[{\frac{10}{3},+∞})$ | D. | [10,+∞) |
6.已知函数f(x)=$\sqrt{3}$sin(2x-φ)-cos(2x-φ)(|φ|<$\frac{π}{2}$)的图象关于y轴对称,则f(x)在区间$[{-\frac{π}{6},\frac{π}{3}}]$上的最大值为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 2 |
7.如图,在棱长均相等的正三棱柱ABC-A1B1C1中,异面直线AA1与BC1的夹角为( )
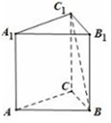

| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
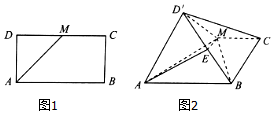 如图,矩形ABCD中,AB=2$\sqrt{2}$,AD=$\sqrt{2}$,M为DC的中点,将△DAM沿AM折到△D′AM的位置,AD′⊥BM.
如图,矩形ABCD中,AB=2$\sqrt{2}$,AD=$\sqrt{2}$,M为DC的中点,将△DAM沿AM折到△D′AM的位置,AD′⊥BM.