题目内容
20.设函数f(x)=$\frac{{x}^{3}}{3}$-$\frac{3a+2}{2}$x2+6ax+b,其中a,b∈R.(1)若函数f(x)在x=1处取得极值-$\frac{1}{6}$,求a,b的值;
(2)求函数f(x)的单调递增区间.
分析 (1)求出f′(x)=x2-(3a+2)x+6a,由函数f(x)在x=1处取得极值-$\frac{1}{6}$,列出方程组,能求出a,b.
(2)由f′(x)=x2-3x+2,利用导数性质能求出函数f(x)的单调递增区间.
解答 解:(1)∵f(x)=$\frac{{x}^{3}}{3}$-$\frac{3a+2}{2}$x2+6ax+b,其中a,b∈R,
∴f′(x)=x2-(3a+2)x+6a,
∵函数f(x)在x=1处取得极值-$\frac{1}{6}$,
∴$\left\{\begin{array}{l}{f(1)=\frac{1}{3}-\frac{3a+2}{2}+6a+b=-\frac{1}{6}}\\{{f}^{'}(1)=1-(3a+2)+6a=0}\end{array}\right.$,
解得a=$\frac{1}{3}$,b=-1.
(2)由(1)得f(x)=$\frac{{x}^{3}}{3}$-$\frac{3}{2}{x}^{2}$+2x-1,
∴f′(x)=x2-3x+2,
由f′(x)=x2-3x+2>0,得x>2或x<1,
∴函数f(x)的单调递增区间为(-∞,1],[2,+∞).
点评 本题考查导数及其应用、不等式、函数等基础知识,考查考查推理论证能力、运算求解能力、抽象概括能力,考查化归与转化思想、函数与方程思想、分类与整合思想,是中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
1.在等比数列{an}中,a1=1,a3=2a2,数列{an}前n项和Sn为( )
| A. | Sn=2n-1 | B. | Sn=2n-1 | C. | Sn=n2 | D. | Sn=2n-1 |
10.现行普通高中学生在高一升高二时面临着选文理科的问题,学校抽取了部分男、女学生意愿的一份样本,制作出如下两个等高堆积条形图:
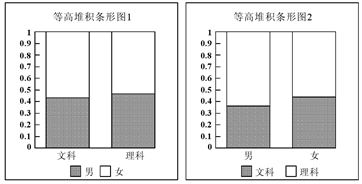
根据这两幅图中的信息,下列哪个统计结论是不正确的( )

根据这两幅图中的信息,下列哪个统计结论是不正确的( )
| A. | 样本中的女生数量多于男生数量 | |
| B. | 样本中有理科意愿的学生数量多于有文科意愿的学生数量 | |
| C. | 样本中的男生偏爱理科 | |
| D. | 样本中的女生偏爱文科 |
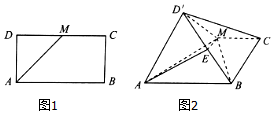 如图,矩形ABCD中,AB=2$\sqrt{2}$,AD=$\sqrt{2}$,M为DC的中点,将△DAM沿AM折到△D′AM的位置,AD′⊥BM.
如图,矩形ABCD中,AB=2$\sqrt{2}$,AD=$\sqrt{2}$,M为DC的中点,将△DAM沿AM折到△D′AM的位置,AD′⊥BM.