题目内容
6.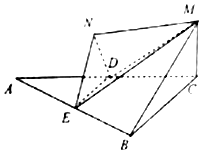 已知如图,△ABC是边长为4的等边三角形,MC⊥平面ABC,D、E分别是线段AC、AB的中点,将△ADE沿DE翻折至△NDE,平面NDE⊥平面ABC.
已知如图,△ABC是边长为4的等边三角形,MC⊥平面ABC,D、E分别是线段AC、AB的中点,将△ADE沿DE翻折至△NDE,平面NDE⊥平面ABC.(Ⅰ)求证:平面BCM∥平面EDN;
(Ⅱ)求三棱锥M-EDN的体积V.
分析 (Ⅰ)推导出MC∥平面EDN,从而BC∥ED,进而BC∥平面NDE,由此能证明平面BCM∥平面EDN.
(Ⅱ) 设BC中点为G,连接AG交DE于F.则AG⊥ED,推导出GF⊥平面NDE,由此能求出三棱锥M-NDE的体积.
解答 证明:(Ⅰ)∵平面EDN⊥平面ABC,MC⊥平面ABC,MC?平面EDN,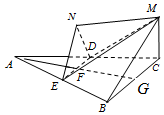
∴MC∥平面EDN.…(2分)
由已知,BC∥ED,∵BC?平面NDE,ED?平面NDE,
∴BC∥平面NDE.…(4分)
∵BC、MC是平面BCM内两相交直线,
∴平面BCM∥平面EDN.…(6分)
解:(Ⅱ) 设BC中点为G,连接AG交DE于F.则AG⊥ED.…(7分)
∵平面EDN⊥平面ABC,平面EDN∩平面ABC=ED,
AG?平面ABC,
∴GF⊥平面NDE.…(9分)
由已知,△NDE的面积S△NDE=$\sqrt{3}$.GF=NF=$\sqrt{3}$,…(11分)
∴三棱锥M-NDE的体积V=$\frac{1}{3}$GF•S△NDE=$\frac{1}{3}$×$\sqrt{3}$×$\sqrt{3}$=1.…(12分)
点评 本题考查面面平行的证明,考查三棱锥的体积的求法,考查推理论证能力、运算求解能力、空间思维能力,考查函数与方程思想、化归转化思想、数形结合思想,是中档题.

练习册系列答案
相关题目
16.已知函数f(x)=2sinxsin(x+3φ)是奇函数,其中$φ∈(0,\frac{π}{2})$,则函数g(x)=cos(2x-φ)的图象( )
| A. | 关于点$(\frac{π}{12},0)$对称 | |
| B. | 关于轴$x=-\frac{5π}{12}$对称 | |
| C. | 可由函数f(x)的图象向右平移$\frac{π}{6}$个单位得到 | |
| D. | 可由函数f(x)的图象向左平移$\frac{π}{3}$个单位得到 |
17.已知集合A=$\{1,2,3,4\},B=\{y|y=\sqrt{x},x∈A\}$,则A∩B=( )
| A. | {1} | B. | {1,2} | C. | {1,4} | D. | {1,2,3,4} |
1.在等比数列{an}中,a1=1,a3=2a2,数列{an}前n项和Sn为( )
| A. | Sn=2n-1 | B. | Sn=2n-1 | C. | Sn=n2 | D. | Sn=2n-1 |
6.已知函数f(x)=$\sqrt{3}$sin(2x-φ)-cos(2x-φ)(|φ|<$\frac{π}{2}$)的图象关于y轴对称,则f(x)在区间$[{-\frac{π}{6},\frac{π}{3}}]$上的最大值为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 2 |