题目内容
若直线l的方程为ax+by+c=0,(a,b不同时为零),则下列命题正确的是 .
(1)以方程ax+by+c=0的解为坐标的点都在直线l上;
(2)方程ax+by+c=0可以表示平面坐标系中的任意一条直线;
(3)直线l的一个法向量为(a,b);
(4)直线l的倾斜角为arctan(-
).
(1)以方程ax+by+c=0的解为坐标的点都在直线l上;
(2)方程ax+by+c=0可以表示平面坐标系中的任意一条直线;
(3)直线l的一个法向量为(a,b);
(4)直线l的倾斜角为arctan(-
| a |
| b |
考点:直线的一般式方程
专题:直线与圆
分析:(1)根据方程的解与直线的坐标的关系即可得出;
(2)方程ax+by+c=0为直线的一般式可以表示平面坐标系中的任意一条直线;
(3)直线l的一个方向向量为(b,-a),可得直线l的一个法向量为(a,b);
(4)直线l的倾斜角为arctan(-
)或π-arctan(
)或
.
(2)方程ax+by+c=0为直线的一般式可以表示平面坐标系中的任意一条直线;
(3)直线l的一个方向向量为(b,-a),可得直线l的一个法向量为(a,b);
(4)直线l的倾斜角为arctan(-
| a |
| b |
| a |
| b |
| π |
| 2 |
解答:
解:直线l的方程为ax+by+c=0,(a,b不同时为零).
(1)以方程ax+by+c=0的解为坐标的点都在直线l上,正确;
(2)方程ax+by+c=0可以表示平面坐标系中的任意一条直线,正确;
(3)直线l的一个方向向量为(b,-a),可得直线l的一个法向量为(a,b),正确;
(4)直线l的倾斜角为arctan(-
)或π-arctan(
)或
,不正确.
综上可得:只有(1)(2)(3)正确.
故答案为:(1)(2)(3).
(1)以方程ax+by+c=0的解为坐标的点都在直线l上,正确;
(2)方程ax+by+c=0可以表示平面坐标系中的任意一条直线,正确;
(3)直线l的一个方向向量为(b,-a),可得直线l的一个法向量为(a,b),正确;
(4)直线l的倾斜角为arctan(-
| a |
| b |
| a |
| b |
| π |
| 2 |
综上可得:只有(1)(2)(3)正确.
故答案为:(1)(2)(3).
点评:本题考查了直线l的方程为ax+by+c=0(a,b不同时为零)的意义、法向量与方向向量的关系、反三角函数,考查了推理能力,属于基础题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
在平面直角坐标系xOy中,设不等式组
,表示的平面区域为D,在D内任取一整点P(横、纵坐标都是整数)测P落在区域
内的概率为( )
|
|
A、
| ||
B、
| ||
C、
| ||
D、
|
将函数y=sin(x+
)cos(x+
)的图象沿x轴向右平移
个单位后,得到一个偶函数的图象,则φ的取值不可能是( )
| φ |
| 2 |
| φ |
| 2 |
| π |
| 8 |
A、
| ||
B、-
| ||
C、
| ||
D、
|
8cos410°-6cos20°+
sin40°=( )
| 3 |
A、
| ||||
| B、3 | ||||
C、
| ||||
D、
|
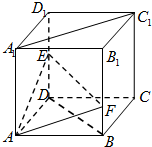 如图,在棱长为a的正方体ABCD-A1B1C1D1中,点E是棱D1D的中点,点F在棱B1B上,
如图,在棱长为a的正方体ABCD-A1B1C1D1中,点E是棱D1D的中点,点F在棱B1B上,