Question

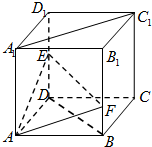如图，在棱长为a的正方体ABCD-A₁B₁C₁D₁中，点E是棱D₁D的中点，点F在棱B₁B上，
（1）当满足B₁F=2FB．在棱C₁C上确定一点G，使A，E，G，F四点共面，并求此时C₁G的长；
（2）当点F在棱B₁B上移动时，求三棱锥F-ADE的体积．

Answer 1

考点：点、线、面间的距离计算,棱柱、棱锥、棱台的体积

专题：空间位置关系与距离

分析：（1）取C₁C的中点H，连结BH，在平面BB₁C₁C中，过点F作FG∥BH，则FG∥AE．连结EG，则A，E，G，F四点共面．由此能求出当C₁G=

1

6

a时，A，E，G，F四点共面．
（2）由已知得S_△ADE=

1

2

×AD×DE=

1

2

a×

1

2

a=

1

4

a2，点F到平面ADE的距离h=a，由此能求出三棱锥F-ADE的体积．

解答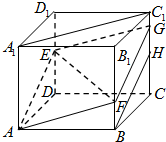： （1）解：取C₁C的中点H，连结BH，则BH∥AE．
在平面BB₁C₁C中，过点F作FG∥BH，则FG∥AE．
连结EG，则A，E，G，F四点共面．
因为CH=

1

2

C₁C=

1

2

a，HG=BF

1

3

C₁C=

1

3

a，
所以C₁G=C₁C-CH-HG=

1

6

a．
故当C₁G=

1

6

a时，A，E，G，F四点共面．
（2）解：∵在棱长为a的正方体ABCD-A₁B₁C₁D₁中，点E是棱D₁D的中点，
∴S_△ADE=

1

2

×AD×DE=

1

2

a×

1

2

a=

1

4

a2，
又∵BB₁∥平面ADE，且BB₁到平面ADE的距离为a，点F在棱B₁B上移动，
∴点F到平面ADE的距离h=a，
∴V_F-ADE=

1

3

S△ADE•h=

1

3

×

a2

4

×a=

a3

12

．

点评：本小题主要考查空间线面关系、几何体的体积等知识，考查数形结合、化归与转化的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力．