题目内容
5.已知函数f(x)=x3+|ax-3|-2,a>0.(1)求函数y=f(x)的单调区间;
(2)当a∈(0,5)时,对于任意x1∈[0,1],总存在x2∈[0,1],使得f(x1)+f(x2)=0,求实数a的值.
分析 (1)讨论当x≥$\frac{3}{a}$时,去掉绝对值,求出导数;当x<$\frac{3}{a}$时,去掉绝对值,求出导数,讨论当0<a≤1时,当1<a≤3时,当a>3时,由导数大于0,可得增区间,导数小于0,可得减区间;
(2)由题意可得f(0)+f(1)=0,求得a的值,去掉绝对值,画出f(x)在[0,1]的图象,即可得到结论.
解答 解:(1)当x≥$\frac{3}{a}$时,f(x)=x3+ax-5,
由a>0,f′(x)=3x2+a>0,可得f(x)在[$\frac{3}{a}$,+∞)递增;
当x<$\frac{3}{a}$时,f(x)=x3-ax+1,
由a>0,f′(x)=3x2-a,
由f′(x)>0,可得x>$\sqrt{\frac{a}{3}}$或x<-$\sqrt{\frac{a}{3}}$;
由f′(x)<0,可得-$\sqrt{\frac{a}{3}}$<x<$\sqrt{\frac{a}{3}}$.
当0<a≤1时,$\sqrt{\frac{a}{3}}$≤$\frac{3}{a}$,f(x)在($\sqrt{\frac{a}{3}}$,$\frac{3}{a}$),(-∞,-$\sqrt{\frac{a}{3}}$)递增;
在(-$\sqrt{\frac{a}{3}}$,$\sqrt{\frac{a}{3}}$)递减;
当a>1时,$\sqrt{\frac{a}{3}}$>$\frac{3}{a}$,f(x)在(-∞,-$\sqrt{\frac{a}{3}}$)递增;
在(-$\sqrt{\frac{a}{3}}$,$\frac{3}{a}$)递减;
综上可得,当0<a≤1时,f(x)的增区间为(-∞,-$\sqrt{\frac{a}{3}}$),($\sqrt{\frac{a}{3}}$,+∞),
减区间为(-$\sqrt{\frac{a}{3}}$,$\sqrt{\frac{a}{3}}$);
当1<a≤3时,f(x)的增区间为(-∞,-$\sqrt{\frac{a}{3}}$),[$\sqrt{\frac{a}{3}}$,+∞),
减区间为(-$\sqrt{\frac{a}{3}}$,$\sqrt{\frac{a}{3}}$);
当a>3时,f(x)的增区间为(-∞,-$\sqrt{\frac{a}{3}}$),[$\frac{3}{a}$,+∞),
减区间为(-$\sqrt{\frac{a}{3}}$,$\frac{3}{a}$);
(2)当a∈(0,5)时,对于任意x1∈[0,1],
总存在x2∈[0,1],使得f(x1)+f(x2)=0,
由f(0)=1,结合图象可得f(1)=1+|a-3|-2=-1,
解得a=3.
当a=3时,f(x)=x3+|3x-3|-2,
当x∈[0,1]时,f(x)=x3-3x+1,
f′(x)=3x2-3≤0,f(x)递减,则f(x)∈[-1,0],且与x轴有一个交点,
故a=3成立.
点评 本题考查导数的运用:求单调区间,注意运用分类讨论思想方法,考查任意性和存在性问题的解法,注意结合图象,考查运算能力,有一定难度.

 名校课堂系列答案
名校课堂系列答案| A. | (-∞,$\frac{1}{e}$] | B. | (-∞,e] | C. | $({\frac{1}{e},+∞})$ | D. | (e,+∞) |
| A. | f(x)=1,g(x)=x0 | B. | f(x)=$\root{3}{x}$,g(x)=$\frac{{x}^{2}}{x}$ | C. | f(x)=lnex,g(x)=elnx | D. | f(x)=$\frac{1}{|x|}$,g(x)=$\frac{1}{\sqrt{{x}^{2}}}$ |
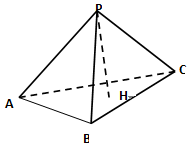 已知P为△ABC所在平面外一点,PA⊥PB,PB⊥PC,PC⊥PA,PH⊥平面 ABC,H,则H为△ABC的( )
已知P为△ABC所在平面外一点,PA⊥PB,PB⊥PC,PC⊥PA,PH⊥平面 ABC,H,则H为△ABC的( )| A. | 重心 | B. | 垂心 | C. | 外心 | D. | 内心 |
| A. | ($\frac{1}{2}$,+∞) | B. | (-∞,$\frac{1}{2}$) | C. | (0,$\frac{2}{3}$) | D. | ($\frac{1}{2}$,1)∪(1,+∞) |
| A. | $2\sqrt{3}$ | B. | $3\sqrt{2}$ | C. | 1 | D. | 2 |
| A. | {0,1,2} | B. | {0,1,2,3} | C. | {0,1} | D. | {1,2} |