题目内容
10．
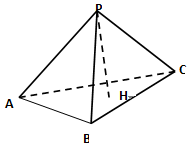已知P为△ABC所在平面外一点，PA⊥PB，PB⊥PC，PC⊥PA，PH⊥平面 ABC，H，则H为△ABC的（ ）| A． | 重心 | B． | 垂心 | C． | 外心 | D． | 内心 |
分析 点P为△ABC所在平面外一点，PH⊥平面ABC，垂足为H，分析可证得BE⊥AC、AD⊥BC，符合这一性质的点H是△ABC垂心
解答 证明：连结AH并延长，交BC与D连结BH并延长，交AC与E；
因PA⊥PB，PA⊥PC，故PA⊥面PBC，故PA⊥BC；
因PH⊥面ABC，故PH⊥BC，故BC⊥面PAH，
故AH⊥BC即AD⊥BC；
同理：BE⊥AC；
故H是△ABC的垂心．
故选：B
点评 本题是立体几何中一道证明题，考查了线面垂直的定义与三角形的全等．
练习册系列答案
100分闯关期末冲刺系列答案
名校联盟快乐课堂系列答案
相关题目
20．
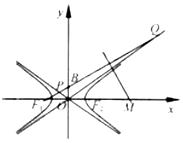如图，F1，F2分别是双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$（a，b＞0）的左、右焦点，B是虚轴的端点，直线F1B与C的两条渐近线分别交于P，Q两点，线段PQ的垂直平分线与x轴交于点M，若|MF2|=|F1F2|，则双曲线C的渐近线方程是（ ）
如图，F1，F2分别是双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$（a，b＞0）的左、右焦点，B是虚轴的端点，直线F1B与C的两条渐近线分别交于P，Q两点，线段PQ的垂直平分线与x轴交于点M，若|MF2|=|F1F2|，则双曲线C的渐近线方程是（ ）| A． | y=±x | B． | $y=±\sqrt{3}x$ | C． | $y=±\frac{1}{2}x$ | D． | $y=±\frac{{\sqrt{2}}}{2}x$ |
15．已知三棱锥P-ABC的三条侧棱PA、PB、PC两两互相垂直，且PA=2，PB=$\sqrt{3}$，PC=3，则这个三棱锥的外接球的表面积为（ ）
| A． | 16π | B． | 32π | C． | 36π | D． | 64π |
2．定义在实数集R上的奇函数分f（x），对任意实数x都有$f（\frac{3}{2}-x）=f（x）$，且满足f（1）＞-2，$f（2）=m-\frac{3}{m}$，则实数m的取值范围是（ ）
| A． | 0＜m＜3或m＜-1 | B． | 0＜m＜3 | C． | -1＜m＜3 | D． | m＞3或m＜-1 |
19．设偶函数f（x）的定义域为R，函数g（x）=$\frac{x}{{{x^2}+1}}$，则下列结论中正确的是（ ）
| A． | |f（x）|g（x）是奇函数 | B． | f（x）g（x）是偶函数 | C． | f（x）|g（x）|是奇函数 | D． | |f（x）g（x）|是奇函数 |