题目内容
若平面向量
与向量
=(-2,1)共线反向,且|
|=2
,则
= .
| b |
| a |
| b |
| 5 |
| b |
考点:平面向量共线(平行)的坐标表示
专题:平面向量及应用
分析:设
=λ
,λ<0,由已知,求出λ,即可得出
的坐标.
| b |
| a |
| b |
解答:
解:设
=λ
,λ<0,由已知
=(-2,1),
∴
=(-2λ,λ),
∵|
|=2
,
∴
=2
,
解得λ=-2,
∴
=(4,-2),
故答案为:(4,-2).
| b |
| a |
| a |
∴
| b |
∵|
| b |
| 5 |
∴
| 4λ2+λ2 |
| 5 |
解得λ=-2,
∴
| b |
故答案为:(4,-2).
点评:本题考查共线向量的坐标表示,向量模的计算,属于基础题.

练习册系列答案
相关题目
已知双曲线
-
=1左、右焦点分别为F1,F2,过点F2作与x轴垂直的直线与双曲线一个交点为P,且∠PF1F2=
,则双曲线的渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 6 |
A、y=±
| ||||
B、y=±
| ||||
C、y=±
| ||||
| D、y=±x |
椭圆x2+4y2=1的离心率为( )
A、
| ||||
B、
| ||||
C、±
| ||||
D、±
|
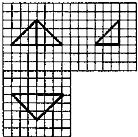 如图,网格纸上小正方形的边长为2,粗线画出的是某几何体的三视图,则此几何体的体积为
如图,网格纸上小正方形的边长为2,粗线画出的是某几何体的三视图,则此几何体的体积为