题目内容
已知函数f(x)=
-alnx.(a∈R)
(1)当a=-1时,试确定函数f(x)在其定义域内的单调性;
(2)求函数f(x)在(0,e)上的最小值.
| 1 |
| x |
(1)当a=-1时,试确定函数f(x)在其定义域内的单调性;
(2)求函数f(x)在(0,e)上的最小值.
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)利用导数与函数单调性的关系即可得出;
(2)利用导数研究其单调性,对分类讨论即可得出.
(2)利用导数研究其单调性,对分类讨论即可得出.
解答:
解:(1)当a=-1时,f(x)=
+lnx,x∈(0,+∞),
则f′(x)=
,
∵当0<x<1时,f'(x)<0,当x>1时,f'(x)>0.
∴函数f(x)在(0,1)上单调递减,在(1,+∞)上单调递增.
(2)∵f′(x)=-
,
①当a≥0时,∵x∈(0,e],∴ax+1>0⇒f'(x)<0,
函数f(x)在(0,e]上单调递减,
∴f(x)min=f(e)=
-a.
②当a<0时,令f'(x)=0得x=-
,
当-
<e,即a<-
时,对x∈(0,-
),有f'(x)<0;即函数f(x)在(0,-
)上单调递减;
对x∈(-
,e),有f'(x)>0,即函数f(x)在(-
,e)上单调递增;
∴f(x)min=f(-
)=-a-aln(-
);
当-
≥e,即a≥-
时,对x∈(0,e]有f'(x)<0,即函数f(x)在(0,e]上单调递减;
∴f(x)min=f(e)=
-a.
综上得f(x)min=
.
| 1 |
| x |
则f′(x)=
| x-1 |
| x2 |
∵当0<x<1时,f'(x)<0,当x>1时,f'(x)>0.
∴函数f(x)在(0,1)上单调递减,在(1,+∞)上单调递增.
(2)∵f′(x)=-
| ax+1 |
| x2 |
①当a≥0时,∵x∈(0,e],∴ax+1>0⇒f'(x)<0,
函数f(x)在(0,e]上单调递减,
∴f(x)min=f(e)=
| 1 |
| e |
②当a<0时,令f'(x)=0得x=-
| 1 |
| a |
当-
| 1 |
| a |
| 1 |
| e |
| 1 |
| a |
| 1 |
| a |
对x∈(-
| 1 |
| a |
| 1 |
| a |
∴f(x)min=f(-
| 1 |
| a |
| 1 |
| a |
当-
| 1 |
| a |
| 1 |
| e |
∴f(x)min=f(e)=
| 1 |
| e |
综上得f(x)min=
|
点评:本题考查了利用导研究函数的单调性、分类讨论思想,是一道综合题.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
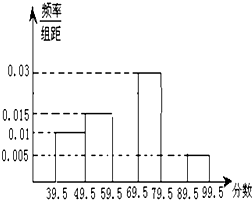 为了解一大片经济林生长情况,随机测量其中的60株的底部周长(单位:cm),规定底部周长60cm及以上优质树木)将周长整理后画出的频率分布表和频率分布直方图如图:观察图形,回答下列问题:
为了解一大片经济林生长情况,随机测量其中的60株的底部周长(单位:cm),规定底部周长60cm及以上优质树木)将周长整理后画出的频率分布表和频率分布直方图如图:观察图形,回答下列问题: