题目内容
函数y=sin(
x+
),x∈[-π,
]的单调递增区间为 .
| 1 |
| 2 |
| π |
| 3 |
| π |
| 2 |
考点:正弦函数的单调性
专题:计算题,三角函数的图像与性质
分析:由x∈[-π,
]⇒
x+
∈[-
,
],利用y=sinx在[-
,
]上单调递增,即可求得答案.
| π |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 6 |
| 7π |
| 12 |
| π |
| 6 |
| π |
| 2 |
解答:
解:∵x∈[-π,
],
∴
x+
∈[-
,
],
∵y=sinx在[-
,
]上单调递增,
∴-
≤
x+
≤
,
解得-π≤x≤
,
∴当x∈[-π,
]时,y=sin(
x+
)的单调递增区间为[-π,
],
故答案为:[-π,
].
| π |
| 2 |
∴
| 1 |
| 2 |
| π |
| 3 |
| π |
| 6 |
| 7π |
| 12 |
∵y=sinx在[-
| π |
| 6 |
| π |
| 2 |
∴-
| π |
| 6 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 2 |
解得-π≤x≤
| π |
| 3 |
∴当x∈[-π,
| π |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
故答案为:[-π,
| π |
| 3 |
点评:本题考查正弦函数的单调性,求得
x+
∈[-
,
]是基础,利用y=sinx在[-
,
]上单调递增解决是关键,属于中档题.
| 1 |
| 2 |
| π |
| 3 |
| π |
| 6 |
| 7π |
| 12 |
| π |
| 6 |
| π |
| 2 |

练习册系列答案
相关题目
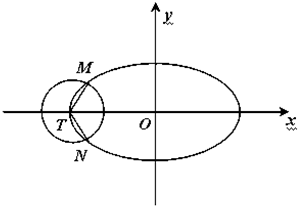 如图,已知椭圆C:
如图,已知椭圆C: