Question

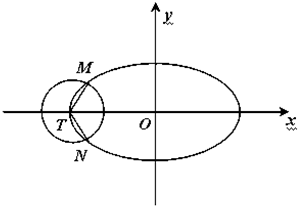如图，已知椭圆C：

x2

a2

+

y2

b2

=1（a＞b＞0）的离心率为

3

2

，以椭圆C的左顶点T为圆心作圆T：（x+2）²+y²=r²（r＞0），设圆T与椭圆C交于点M与点N．
（1）求椭圆C的标准方程；
（2）求

TM

•

TN

的最小值，并求此时圆T的方程．

Answer 1

考点：直线与圆锥曲线的关系,椭圆的标准方程

专题：综合题,圆锥曲线的定义、性质与方程

分析：（1）利用椭圆的离心率为

3

2

，a=2，可求椭圆C的标准方程；
（2）根据点M与点N关于x轴对称，利用直角坐标方程或参数方程，设出N的坐标，再利用点M在椭圆C上，利用数量积的坐标表达式得出

TM

•

TN

的表达式，最后利用二次函数的性质求其最小值及求此时圆T的方程．

解答： 解：（1）依题意，得a=2，e=

c

a

=

3

2

，∴c=

3

， b=

a2-c2

=1；
故椭圆C的方程为

x2

4

+y2=1．
（2）点M与点N关于x轴对称，故设M（2cosθ，sinθ），N（2cosθ，-sinθ），
不妨设sinθ＞0，由已知T（-2，0），
则

TM

•

TN

=（2cosθ+2，sinθ）•（2cosθ+2，-sinθ）=（2cosθ+2）²-sin²θ=5cos²θ+8cosθ+3
=5(cosθ+

4

5

)2-

1

5

．
故当cosθ=-

4

5

时，

TM

•

TN

取得最小值为-

1

5

，此时M（-

8

5

，

3

5

），
又点M在圆T上，代入圆的方程得到r²=

13

25

．
故圆：（x+2）²+y²=

13

25

．

点评：本题考查椭圆的方程和几何性质、圆的方程等基础知识，考查向量的数量积公式，考查运算求解能力、推理论证能力，属于中档题．