题目内容
若二次函数f（x）的图象与x轴有两个相异交点，它的导函数f′（x）的图象过二、三、四象限，则函数f（x）图象的顶点在第 象限．
考点：导数的运算
专题：导数的概念及应用
分析：设二次函数y=f（x）=ax2+bx，利用它的导数y=f′（x）=2ax+b 图象过二、三、四象限，可得a＜0，b＜0，y=f（x）的图象顶点 （-
，
）在第二象限．
| b |
| 2a |
| -b2 |
| 4a |
解答：
解：由题意可知可设二次函数y=f（x）=ax2+bx，它的导数y=f′（x）=2ax+b，
由导数y=f′（x）的图象是经过二、三、四象限的一条直线，
∴a＜0，b＜0，
y=f（x）的图象顶点 （-
，
）在第二象限，
故答案为：二．
由导数y=f′（x）的图象是经过二、三、四象限的一条直线，
∴a＜0，b＜0，
y=f（x）的图象顶点 （-
| b |
| 2a |
| -b2 |
| 4a |
故答案为：二．
点评：本题考查求函数的导数的方法，直线在坐标系中的位置与斜率、截距的关系，二次函数的性质．
练习册系列答案
相关题目
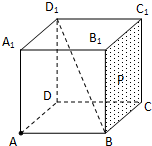如图，棱长为1的正方体ABCD-A1B1C1D1中，点P在侧面BCC1B1及其边界上运动，并且总保持向量椭圆
+
=1与双曲线
-
=1有相同的焦点，则实数m的值为（ ）
| x2 |
| 9 |
| y2 |
| m2 |
| x2 |
| m |
| y2 |
| 3 |
| A、2 | B、-2 | C、-3 | D、4 |