题目内容
已知数列{an}是公差d不为零的等差数列,{bn}是等比数列,函数f(x)=b1x2+b2x+b3的图象在y轴上的截距为-4,其最大值为a6-
.
(Ⅰ)求a6的值;
(Ⅱ)若f(a2+a8)=f(a3+a11),求数列{bn}的通项公式;
(Ⅲ)若a2=-
,设Tn为数列{
}的前n项和,若Tn=-
,求正整数n的值.
| 7 |
| 2 |
(Ⅰ)求a6的值;
(Ⅱ)若f(a2+a8)=f(a3+a11),求数列{bn}的通项公式;
(Ⅲ)若a2=-
| 7 |
| 2 |
| 1 |
| anan+1 |
| 4 |
| 9 |
考点:数列的求和,数列与函数的综合
专题:等差数列与等比数列
分析:(I)由于函数f(x)=b1x2+b2x+b3的图象在y轴上的截距为-4,其最大值为a6-
.可得b3=-4,且当x=-
时,函数f(x)取得最大值
=b3-
b3=a6-
,解得a6.
(II)由f(a2+a8)=f(a3+a11),可得
=-
.化为-
=
,即可解得
.
(Ⅲ)由于a2=-
,a6=
,可得公差d=
=1,即可得出an=
.可得
=
=
-
.利用“裂项求和”可得数列{
}的前n项和Tn=-
-
.由于Tn=-
,令-
=-
-
,解得n即可.
| 7 |
| 2 |
| b2 |
| 2b1 |
4b1b3-
| ||
| 4b1 |
| 1 |
| 4 |
| 7 |
| 2 |
(II)由f(a2+a8)=f(a3+a11),可得
| a2+a8+a3+a11 |
| 2 |
| b2 |
| 2b1 |
| b2 |
| 2b1 |
| 4a6 |
| 2 |
| b2 |
| b1 |
(Ⅲ)由于a2=-
| 7 |
| 2 |
| 1 |
| 2 |
| a6-a2 |
| 4 |
| 2n-11 |
| 2 |
| 1 |
| anan+1 |
| 4 |
| (2n-11)(2n-9) |
| 1 |
| 2n-11 |
| 1 |
| 2n-9 |
| 1 |
| anan+1 |
| 1 |
| 9 |
| 1 |
| 2n-9 |
| 4 |
| 9 |
| 4 |
| 9 |
| 1 |
| 9 |
| 1 |
| 2n-9 |
解答:
解:(I)∵函数f(x)=b1x2+b2x+b3的图象在y轴上的截距为-4,其最大值为a6-
.
∴b3=-4,当x=-
时,函数f(x)取得最大值
=b3-
b3=-4+1=-3=a6-
,解得a6=
.
(II)∵f(a2+a8)=f(a3+a11),∴
=-
.∴-
=
=2a6=1,
∴公比q=
=-2.
∴数列{bn}的通项公式bn=b3•qn-3=-4×(-2)n-3=-(-2)n-1.
(Ⅲ)∵a2=-
,a6=
,∴公差d=
=1,∴an=a2+(n-2)d=-
+n-2=n-
=
.
=
=
-
.
∴数列{
}的前n项和Tn=(
-
)+(
-
)+…+(
-
)=-
-
.
∵Tn=-
,∴-
=-
-
,解得n=6.
| 7 |
| 2 |
∴b3=-4,当x=-
| b2 |
| 2b1 |
4b1b3-
| ||
| 4b1 |
| 1 |
| 4 |
| 7 |
| 2 |
| 1 |
| 2 |
(II)∵f(a2+a8)=f(a3+a11),∴
| a2+a8+a3+a11 |
| 2 |
| b2 |
| 2b1 |
| b2 |
| 2b1 |
| 4a6 |
| 2 |
∴公比q=
| b2 |
| b1 |
∴数列{bn}的通项公式bn=b3•qn-3=-4×(-2)n-3=-(-2)n-1.
(Ⅲ)∵a2=-
| 7 |
| 2 |
| 1 |
| 2 |
| a6-a2 |
| 4 |
| 7 |
| 2 |
| 11 |
| 2 |
| 2n-11 |
| 2 |
| 1 |
| anan+1 |
| 4 |
| (2n-11)(2n-9) |
| 1 |
| 2n-11 |
| 1 |
| 2n-9 |
∴数列{
| 1 |
| anan+1 |
| 1 |
| -9 |
| 1 |
| -7 |
| 1 |
| -7 |
| 1 |
| -5 |
| 1 |
| 2n-11 |
| 1 |
| 2n-9 |
| 1 |
| 9 |
| 1 |
| 2n-9 |
∵Tn=-
| 4 |
| 9 |
| 4 |
| 9 |
| 1 |
| 9 |
| 1 |
| 2n-9 |
点评:本题综合考查了二次函数的性质、等差数列与等比数列的通项公式、“裂项求和”,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
下列命题中是真命题的是( )
| A、任何实数都有算术平方根 |
| B、存在三个实数,它们的和与积相等 |
| C、椭圆的离心率e越接近1时越扁,当e=1时为线段F2F2 |
| D、任意一个无理数,其平方后仍为无理数 |
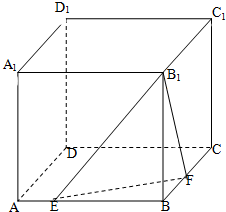 棱长为m的正方体ABCD-A1B1C1D1,E、F分别是棱AB,BC上的动点,且AE=BF.
棱长为m的正方体ABCD-A1B1C1D1,E、F分别是棱AB,BC上的动点,且AE=BF.