题目内容
已知函数y=3sin(
+
)
(1)写出它的振幅、周期、频率和初相;
(2)在直角坐标系中,用“五点法”画出函数y=f(x)一个周期闭区间上的图象;
(3)求函数f(x)的单调递增区间.
| x |
| 2 |
| π |
| 3 |
(1)写出它的振幅、周期、频率和初相;
(2)在直角坐标系中,用“五点法”画出函数y=f(x)一个周期闭区间上的图象;
(3)求函数f(x)的单调递增区间.
考点:正弦函数的图象,五点法作函数y=Asin(ωx+φ)的图象
专题:三角函数的图像与性质
分析:(1)直接结合所给函数的解析式进行求解即可;
(2)直接根据“五点法”画图的步骤进行求解;
(3)直接根据正弦函数的单调性进行求解.
(2)直接根据“五点法”画图的步骤进行求解;
(3)直接根据正弦函数的单调性进行求解.
解答:
解:(1)∵函数y=3sin(
+
),
振幅为3,周期是4π,初相是
,
(2)利用五点法,计算是你如下所示:
当
x+
=0时,x=-
,y=0,
当
x+
=
时,x=
,y=3,
当
x+
=π时,x=
,y=0,
当
x+
=
时,x=
,y=-3,
当
x+
=2π时,x=
,y=0,
函数在一个周期内的图象如下图所示:
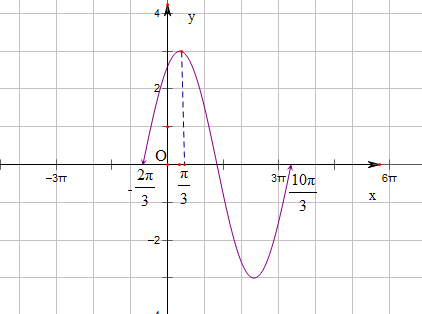
(3)令-
+2kπ≤
x+
≤
+2kπ,k∈Z,
∴-
π+4kπ≤x≤
+4kπ,
∴增区间为[-
π+4kπ,
+4kπ],k∈Z,
| x |
| 2 |
| π |
| 3 |
振幅为3,周期是4π,初相是
| π |
| 3 |
(2)利用五点法,计算是你如下所示:
当
| 1 |
| 2 |
| π |
| 3 |
| 2π |
| 3 |
当
| 1 |
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
当
| 1 |
| 2 |
| π |
| 3 |
| 4π |
| 3 |
当
| 1 |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
| 7π |
| 3 |
当
| 1 |
| 2 |
| π |
| 3 |
| 10π |
| 3 |
函数在一个周期内的图象如下图所示:

(3)令-
| π |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 2 |
∴-
| 5 |
| 3 |
| π |
| 3 |
∴增区间为[-
| 5 |
| 3 |
| π |
| 3 |
点评:本题重点考查了三角函数的图象与性质、三角函数中有关量之间的关系等炸死,属于基础题.解题关键是灵活运用有关性质进行求解.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
下列命题中是真命题的是( )
| A、任何实数都有算术平方根 |
| B、存在三个实数,它们的和与积相等 |
| C、椭圆的离心率e越接近1时越扁,当e=1时为线段F2F2 |
| D、任意一个无理数,其平方后仍为无理数 |
已知向量
,
满足|
|=2,
与
的夹角为60°,则
在
上的投影是( )
| a |
| b |
| b |
| a |
| b |
| b |
| a |
| A、1 | B、2 | C、3 | D、-1 |
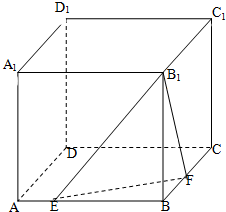 棱长为m的正方体ABCD-A1B1C1D1,E、F分别是棱AB,BC上的动点,且AE=BF.
棱长为m的正方体ABCD-A1B1C1D1,E、F分别是棱AB,BC上的动点,且AE=BF.