题目内容
椭圆
+
=1与双曲线
-
=1有相同的焦点,则实数m的值为( )
| x2 |
| 9 |
| y2 |
| m2 |
| x2 |
| m |
| y2 |
| 3 |
| A、2 | B、-2 | C、-3 | D、4 |
考点:双曲线的简单性质,椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:先根据椭圆的方程求得焦点坐标,进而可知双曲线的半焦距,根据双曲线的标准方程,求得m,答案可得.
解答:
解:椭圆
+
=1得
∴c1=
,
∴焦点坐标为(
,0)(-
,0),
双曲线:
-
=1的焦点必在x轴上,
则半焦距c2=
∴
=
解得实数m=2.
故选:A.
| x2 |
| 9 |
| y2 |
| m2 |
∴c1=
| 9-m2 |
∴焦点坐标为(
| 9-m2 |
| 9-m2 |
双曲线:
| x2 |
| m |
| y2 |
| 3 |
则半焦距c2=
| m+3 |
∴
| m+3 |
| 9-m2 |
解得实数m=2.
故选:A.
点评:此题考查学生掌握圆锥曲线的共同特征,考查椭圆、双曲线的标准方程,以及椭圆、双曲线的简单性质的应用,利用条件求出a,b,c值,是解题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
若x1,x2是方程x2-mx+1-m2=0(m∈R)的实根,则x12+x22的最小值是( )
| A、-2 | ||
B、
| ||
| C、0 | ||
| D、1 |
已知a,b均为正数,
+
=1,则使a+b≥c恒成立的实数c的取值范围是( )
| 1 |
| a |
| 4 |
| b |
| A、c≤9 | B、c≥9 |
| C、c≤10 | D、c≥10 |
已知向量
,
满足|
|=2,
与
的夹角为60°,则
在
上的投影是( )
| a |
| b |
| b |
| a |
| b |
| b |
| a |
| A、1 | B、2 | C、3 | D、-1 |
设f(x)为定义在R上的奇函数,当x≥0时,f(x)=3x+3x+b(b为常数),则f(-1)=( )
| A、5 | B、6 | C、-6 | D、-5 |
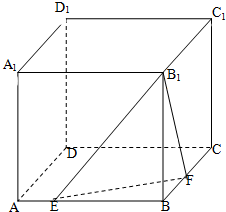 棱长为m的正方体ABCD-A1B1C1D1,E、F分别是棱AB,BC上的动点,且AE=BF.
棱长为m的正方体ABCD-A1B1C1D1,E、F分别是棱AB,BC上的动点,且AE=BF.