题目内容
已知数列{an}的各项均为正数,记A(k)=a1+a2+…+ak,B(k)=a2+a3+…+ak+1C(k)=a3+a4+…+ak+2
(1)若an=
+
,求
B(n);
(2)若a1=1,a2=5,且对任意k∈N*,B(k)都是A(k)与C(k)的等差中项,求数列{an}的通项公式;
(3)已知命题:“若数列{an}是公比为q的等比数列,则对任意k∈N*,A(k),B(k),C(k)都是公比为q的等比数列”是真命题,试写出该命题的逆命题,判断真假,并证明.
(1)若an=
| 1 |
| 3n |
| 1 |
| (-5)n |
| lim |
| n→∞ |
(2)若a1=1,a2=5,且对任意k∈N*,B(k)都是A(k)与C(k)的等差中项,求数列{an}的通项公式;
(3)已知命题:“若数列{an}是公比为q的等比数列,则对任意k∈N*,A(k),B(k),C(k)都是公比为q的等比数列”是真命题,试写出该命题的逆命题,判断真假,并证明.
考点:数列的极限,复合命题的真假
专题:证明题,等差数列与等比数列,简易逻辑
分析:(1)首项利用分组求和法得到B(k)=a2+a3+…+ak+1=(
+
+…+
)+(
+
+…+
),再利用无穷递缩等比数列的和的极限公式即可求得答案;
(2)写出原命题:“若数列{an}是公比为q的等比数列,则对任意k∈N*,A(k),B(k),C(k)都是公比为q的等比数列”的逆命题,判断其为真命题,再证明即可.
| 1 |
| 32 |
| 1 |
| 33 |
| 1 |
| 3k+1 |
| 1 |
| (-5)1 |
| 1 |
| (-5)2 |
| 1 |
| (-5)k+1 |
(2)写出原命题:“若数列{an}是公比为q的等比数列,则对任意k∈N*,A(k),B(k),C(k)都是公比为q的等比数列”的逆命题,判断其为真命题,再证明即可.
解答:
解:(1)∵an=
+
,B(k)=a2+a3+…+ak+1=(
+
+…+
)+(
+
+…+
)
∴
B(n)=
+
=
…3分
(2)对任意k∈N*,A(k)、B(k)、C(k)是等差数列,所以B(k)-A(k)=C(k)-B(k),即ak+1-a1=ak+2-a2,∴ak+2-ak+1=a2-a1=4,
故数列{an}是以1为首项,4为公差的等差数列,于是an=1+(n-1)×4=4n-3…6分
(3)逆命题:“若对任意k∈N*,A(k),B(k),C(k)都是公比为q的等比数列,则数列{an}是公比为q的等比数列”该命题为真命题,证明如下:
∵对任意k∈N*,三个数A(k),B(k),C(k)都是公比为q的等比数列,则B(k)=qA(k),C(k)=qB(k),从而C(k)-B(k)=q[B(k)-A(k)],
∴ak+2-a2=q(ak+1-a1),即ak+2-qak+1=a2-qa1,…9分
由n=1有B(1)=qA(1),即a2-qa1,从而ak+2-qak+1=a2-qa1=0,因为ak>0,
所以,
=
=q,故数列{an}是公比为q的等比数列,得证…12分
| 1 |
| 3n |
| 1 |
| (-5)n |
| 1 |
| 32 |
| 1 |
| 33 |
| 1 |
| 3k+1 |
| 1 |
| (-5)1 |
| 1 |
| (-5)2 |
| 1 |
| (-5)k+1 |
∴
| lim |
| n→∞ |
| ||
1-
|
| ||
1+
|
| 1 |
| 5 |
(2)对任意k∈N*,A(k)、B(k)、C(k)是等差数列,所以B(k)-A(k)=C(k)-B(k),即ak+1-a1=ak+2-a2,∴ak+2-ak+1=a2-a1=4,
故数列{an}是以1为首项,4为公差的等差数列,于是an=1+(n-1)×4=4n-3…6分
(3)逆命题:“若对任意k∈N*,A(k),B(k),C(k)都是公比为q的等比数列,则数列{an}是公比为q的等比数列”该命题为真命题,证明如下:
∵对任意k∈N*,三个数A(k),B(k),C(k)都是公比为q的等比数列,则B(k)=qA(k),C(k)=qB(k),从而C(k)-B(k)=q[B(k)-A(k)],
∴ak+2-a2=q(ak+1-a1),即ak+2-qak+1=a2-qa1,…9分
由n=1有B(1)=qA(1),即a2-qa1,从而ak+2-qak+1=a2-qa1=0,因为ak>0,
所以,
| ak+2 |
| ak+1 |
| a2 |
| a1 |
点评:本题考查数列的极限,考查数列的分组求和与公式法求和,考查等差数列的关系的确定与等比数列的性质的应用,考查推理证明能力,是难题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
若x1,x2是方程x2-mx+1-m2=0(m∈R)的实根,则x12+x22的最小值是( )
| A、-2 | ||
B、
| ||
| C、0 | ||
| D、1 |
已知a,b均为正数,
+
=1,则使a+b≥c恒成立的实数c的取值范围是( )
| 1 |
| a |
| 4 |
| b |
| A、c≤9 | B、c≥9 |
| C、c≤10 | D、c≥10 |
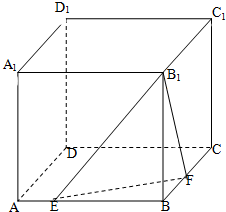 棱长为m的正方体ABCD-A1B1C1D1,E、F分别是棱AB,BC上的动点,且AE=BF.
棱长为m的正方体ABCD-A1B1C1D1,E、F分别是棱AB,BC上的动点,且AE=BF.