Question

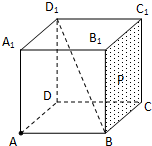如图，棱长为1的正方体ABCD-A₁B₁C₁D₁中，点P在侧面BCC₁B₁及其边界上运动，并且总保持向量

AP

在

BD1

上的投影为0，则线段AP扫过的区域的面积为（　　）

• A、

  1

  2

• B、

  2

  2

• C、

  3

  2

• D、

  5

  4

Answer 1

考点：平行投影及平行投影作图法

专题：空间位置关系与距离

分析：向量

AP

在

BD1

上的投影为0，则等价为AP⊥BD₁，根据条件可知点P的轨迹为面ACB₁与面BCC₁B₁的交线段CB₁

解答： 解：∵点P在侧面BCC₁B₁及其边界上运动，并且总保持向量

AP

在

BD1

上的投影为0，
∴等价为AP⊥BD₁，
连接AC，AB₁，B₁C，
在正方体ABCD-A₁B₁C₁D₁中，
易得BD₁⊥CB₁，BD₁⊥AC；
则BD₁⊥面ACB₁，
又点P在侧面BCC₁B₁及其边界上运动，
根据平面的基本性质得：
点P的轨迹为面ACB₁与面BCC₁B₁的交线段CB₁．
则线段AP扫过的区域为三角形AB₁C，为边长为

2

的正三角形，
则三角形的面积S=

1

2

×(

2

)2×

3

2

=

3

2

，
故选：C

点评：本题主要考查三角形的面积的计算，根据线面垂直的性质确定P的轨迹是解决本题的关键．