题目内容
15.已知f(x)=ex-x,g(x)=lnx+x+1,命题p:?x∈R,f(x)>0,命题q:?x0∈(0,+∞),使得g(x0)=0,则下列说法正确的是( )| A. | p是真命题,¬p:?x0∈R,f(x0)<0 | B. | p是假命题,¬p:?x0∈R,f(x0)≤0 | ||
| C. | q是真命题,¬q:?x∈(0,+∞),g(x)≠0 | D. | q是假命题,¬q:?x∈(0,+∞),g(x)≠0 |
分析 利用导数和函数零点存在条件分别判断命题p,q的真假,结合含有量词的命题的否定进行判断即可.
解答 解:f′(x)=ex-1,由f′(x)>0得x>0,由f′(x)<0得x<0,
即当x=0时,函数f(x)取得极小值,同时也是最小值f(0)=e0-0=1-0=1>0,
∴?x∈R,f(x)>0成立,即p是真命题.
g(x)=lnx+x+1在(0,+∞)上为增函数,当x→0时,g(x)<0,g(1)=0+1+1=2>0,
则:?x0∈(0,+∞),使得g(x0)=0成立,即命题q是真命题.
则¬p:?x0∈R,f(x0)≤0,
¬q:?x∈(0,+∞),g(x)≠0,
综上只有C成立,
故选:C
点评 本题主要考查命题的真假判断以及含有量词的命题的否定,利用函数的性质进行判断是解决本题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
6.f(x)为定义在R上的奇函数,当x>0时,f(x)=lnx,则f(x)>0的解集为( )
| A. | (1,+∞) | B. | (0,1)∪(1,+∞) | C. | (-1,0)∪(1,+∞) | D. | (-∞,-1)∪(1,+∞) |
20.已知平面向量$\overrightarrow a,\overrightarrow b,\overrightarrow c$满足$\overrightarrow c=x\overrightarrow a+y\overrightarrow b$(x,y∈R),且$\overrightarrow a•\overrightarrow c>0$,$\overrightarrow b•\overrightarrow c>0$.( )
| A. | 若$\overrightarrow a•\overrightarrow b<0$,则x>0,y>0 | B. | 若$\overrightarrow a•\overrightarrow b<0$,则x<0,y<0 | ||
| C. | 若$\overrightarrow a•\overrightarrow b>0$,则x<0,y<0 | D. | 若$\overrightarrow a•\overrightarrow b>0$,则x>0,y>0 |
7.函数f(x)=$\frac{1}{x^2-x}$+$\sqrt{2-x}$的定义域是( )
| A. | (-∞,1)∪(1,2) | B. | (-∞,0)∪(0,1)∪(1,2) | C. | (-∞,0)∪(1,2) | D. | (-∞,0)∪(0,1)∪(1,2] |
4.若实数x,y满足不等式组$\left\{\begin{array}{l}x+y≤1\\ x-y≤1\\ x≥0\end{array}\right.$,则2x+y的最大值是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
5.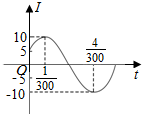 电流强度I(安)随时间t(秒)变化的函数I=Asin(ωt+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的图象如右图所示,则当t=$\frac{1}{100}$秒时,电流强度是( )
电流强度I(安)随时间t(秒)变化的函数I=Asin(ωt+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的图象如右图所示,则当t=$\frac{1}{100}$秒时,电流强度是( )
 电流强度I(安)随时间t(秒)变化的函数I=Asin(ωt+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的图象如右图所示,则当t=$\frac{1}{100}$秒时,电流强度是( )
电流强度I(安)随时间t(秒)变化的函数I=Asin(ωt+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的图象如右图所示,则当t=$\frac{1}{100}$秒时,电流强度是( )| A. | -5 A | B. | 5A | C. | 5$\sqrt{3}$ A | D. | 10 A |