题目内容
5.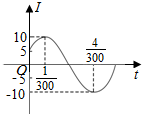 电流强度I(安)随时间t(秒)变化的函数I=Asin(ωt+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的图象如右图所示,则当t=$\frac{1}{100}$秒时,电流强度是( )
电流强度I(安)随时间t(秒)变化的函数I=Asin(ωt+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的图象如右图所示,则当t=$\frac{1}{100}$秒时,电流强度是( )| A. | -5 A | B. | 5A | C. | 5$\sqrt{3}$ A | D. | 10 A |
分析 通过函数的图象求出A,T,然后利用周期公式求出ω,($\frac{1}{300}$,10)为五点中的第二个点,代入表达式,即可求出φ的值,得到函数解析式,代入t=$\frac{1}{100}$秒,即可求出电流强度.
解答 解:由图象可知A=10,$\frac{T}{2}=\frac{4}{300}-\frac{1}{300}=\frac{1}{100}$,
∴ω=$\frac{2π}{T}=100π$,∴函数I=10sin(100πt+φ).
($\frac{1}{300}$,10)为五点中的第二个点,
∴100π×$\frac{1}{300}$+φ=$\frac{π}{2}$,
∵0<φ<$\frac{π}{2}$,
∴φ=$\frac{π}{6}$,I=10sin(100πt+$\frac{π}{6}$).
当t=$\frac{1}{100}$秒时,I=-5安.
故选:A.
点评 本题是基础题,考查学生视图能力,考查由y=Asin(ωx+φ)的部分图象确定其解析式,此是近几年高考中对三角函数的图象与性质考查的一种较热的题型,注意把握其解题规律.注意隐含条件0<φ<$\frac{π}{2}$的应用.

练习册系列答案
相关题目
15.已知f(x)=ex-x,g(x)=lnx+x+1,命题p:?x∈R,f(x)>0,命题q:?x0∈(0,+∞),使得g(x0)=0,则下列说法正确的是( )
| A. | p是真命题,¬p:?x0∈R,f(x0)<0 | B. | p是假命题,¬p:?x0∈R,f(x0)≤0 | ||
| C. | q是真命题,¬q:?x∈(0,+∞),g(x)≠0 | D. | q是假命题,¬q:?x∈(0,+∞),g(x)≠0 |
16.已知对于圆x2+y2-2y=0上任意一点P,不等式x+y+m≥0恒成立,则实数m的取值范围为( )
| A. | m≥-1 | B. | m≥$\sqrt{2}$-1 | C. | m≤-$\sqrt{2}$-1 | D. | m≥$\sqrt{2}-1或m≤-\sqrt{2}$-1 |
13.下列各式中,最小值为2的是( )
| A. | $\frac{x}{y}+\frac{y}{x}$ | B. | $\frac{{{x^2}+3}}{{\sqrt{{x^2}+2}}}$ | C. | 5x+5-x | D. | tanx+cotx |
20.命题“所有奇数的立方是奇数”的否定是( )
| A. | 所有奇数的立方不是奇数 | B. | 不存在一个奇数,它的立方是偶数 | ||
| C. | 存在一个奇数,它的立方是偶数 | D. | 不存在一个奇数,它的立方是奇数 |
10.执行如图所示的程序框图,则输出的s的值为( )


| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
17.执行如图所示的程序框图,则输出的结果是( )


| A. | 21 | B. | 34 | C. | 55 | D. | 89 |
14.函数y=cos($\frac{π}{4}$-2x)的单调递减区间是( )
| A. | [$\frac{π}{8}$+2kπ,$\frac{5π}{8}$+2kπ](k∈Z) | B. | [$\frac{π}{8}$+kπ,$\frac{5π}{8}$+kπ](k∈Z) | ||
| C. | [-$\frac{3π}{8}$+2kπ,$\frac{π}{8}$+2kπ](k∈Z) | D. | [-$\frac{3π}{8}$+kπ,$\frac{π}{8}$+kπ](k∈Z) |
15.在圆C:(x-2)2+(y-2)2=8内,过点P(1,1)的最长的弦为AB,最短的弦为DE,则四边形ADBE的面积为( )
| A. | 2$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 8$\sqrt{3}$ | D. | 16$\sqrt{3}$ |