题目内容
若复数z满足:z+|z|=1+2i,则z的虚部为( )
| A、2i | B、1 | C、2 | D、i |
考点:复数相等的充要条件
专题:数系的扩充和复数
分析:设出复数z的代数形式,代入已知的等式,由复数相等的条件求得z的虚部.
解答:
解:设z=a+bi(a,b∈R),
代入z+|z|=1+2i,得:
a+bi+
=1+2i,
∴
,
∴z的虚部为2.
故选:C.
代入z+|z|=1+2i,得:
a+bi+
| a2+b2 |
∴
|
∴z的虚部为2.
故选:C.
点评:本题考查了复数模的求法,考查了复数相等的充要条件,是基础题.

练习册系列答案
相关题目
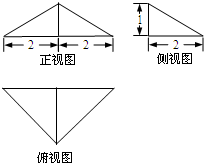
某三棱锥的三视图如图所示,则该几何体的体积为( )

A、
| ||
B、
| ||
C、
| ||
| D、4 |
二次函数y=ax2+bx与指数函数y=(-
)x的图象只可能是( )
| b |
| a |
A、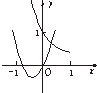 |
B、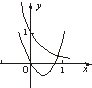 |
C、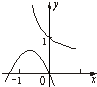 |
D、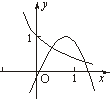 |
设α,β为锐角,那么“sin2α+sin2β=sin(α+β)”是“α+β=
”的( )
| π |
| 2 |
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |