题目内容
从一批苹果中,随机抽取50个,其重量(单位:克)的频数分布图如下:
(1)用分层抽样的方法从重量在[120,125)和[135,140)的苹果中共抽取6个,其重量在[120,125)的有几个?
(2)在(1)中抽出的6个苹果中,任取2个,求重量在[120,125)和[135,140)重各有1的概率.
| 分数(重量) | [120,125) | [125,130) | [130,135) | [135,140] |
| 频数(个) | 5 | 15 | 20 | 10 |
(2)在(1)中抽出的6个苹果中,任取2个,求重量在[120,125)和[135,140)重各有1的概率.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:(1)分层抽样要求各层按照比例抽样即可,(2),共有6个元素,求其概率,列举法求解即可.
解答:
解:(1)若采用分层抽样的方法从重量在[120,125)和[135,140]的苹果中共抽取6个,则重量在[120,125)的个数=
×5=2.
(2)设在[120,125)中抽取的二个苹果为a1,a2,在[135,140]中抽取的四个苹果分别为b1,b2,b3,b4,从抽出的6个苹果中,任取2个共有(a1,a2),(a1,b1),(a1,b2),(a1,b3),(a1,b4),(a2,b1),(a2,b2),(a2,b3),(a2,b4),(b1,b2),(b1,b3),(b1,b4),(b2,b3),(b2,b4),(b3,b4),共15种情况,其中符合“重量在[120,125)和[135,140]中各有一个”的情况共有(a1,b1),(a1,b2),(a1,b3),(a1,b4),(a2,b1),(a2,b2),(a2,b3),(a2,b4)种;设“抽出的4个苹果中,任取2个,求重量在[120,125)和[135,140]中各有一个”为事件A,则事件A的概率P(A)=
.
| 6 |
| 5+10 |
(2)设在[120,125)中抽取的二个苹果为a1,a2,在[135,140]中抽取的四个苹果分别为b1,b2,b3,b4,从抽出的6个苹果中,任取2个共有(a1,a2),(a1,b1),(a1,b2),(a1,b3),(a1,b4),(a2,b1),(a2,b2),(a2,b3),(a2,b4),(b1,b2),(b1,b3),(b1,b4),(b2,b3),(b2,b4),(b3,b4),共15种情况,其中符合“重量在[120,125)和[135,140]中各有一个”的情况共有(a1,b1),(a1,b2),(a1,b3),(a1,b4),(a2,b1),(a2,b2),(a2,b3),(a2,b4)种;设“抽出的4个苹果中,任取2个,求重量在[120,125)和[135,140]中各有一个”为事件A,则事件A的概率P(A)=
| 8 |
| 15 |
点评:本题综合考查统计和概率,注意在(2)中使用列举法时要有逻辑顺序,做到不重不漏.

练习册系列答案
相关题目
设集合M={x|x2-2x-3<0},N={x|log2(1-x)<1},则M∩∁RN等于( )
| A、[-1,1] |
| B、(-1,0) |
| C、[1,3) |
| D、(0,1) |
若复数z满足:z+|z|=1+2i,则z的虚部为( )
| A、2i | B、1 | C、2 | D、i |
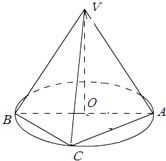 如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,已知AB=2,VA=VB=VC=2.
如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,已知AB=2,VA=VB=VC=2.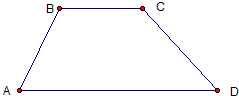 如图,已知
如图,已知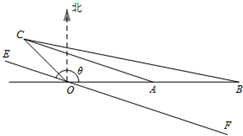 如图,O为总信号源点,A,B,C是三个居民区,已知A,B都在O的正东方向上,OA=10km,OB=20km,C在O的北偏西45°方向上,CO=5
如图,O为总信号源点,A,B,C是三个居民区,已知A,B都在O的正东方向上,OA=10km,OB=20km,C在O的北偏西45°方向上,CO=5