题目内容
二次函数y=ax2+bx与指数函数y=（-
）x的图象只可能是（ ）
| b |
| a |
A、 |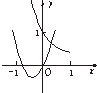
B、 |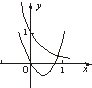
C、 |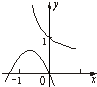
D、 |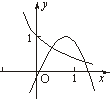
考点：指数函数的图像变换
专题：综合题,函数的性质及应用
分析：根据二次函数的对称轴首先排除A与C选项，再根据a-b的值的正负，结合二次函数和指数函数的性质检验即可得出答案．
解答：
解：根据指数函数y=（-
）x可知a，b异号且不相等
则二次函数y=ax2+bx的对称轴-
＞0可排除A与C
选项D，a-b＞0，a＜0，∴-
＞1，则指数函数单调递增，故D不正确
故选：B．
| b |
| a |
则二次函数y=ax2+bx的对称轴-
| b |
| 2a |
选项D，a-b＞0，a＜0，∴-
| b |
| a |
故选：B．
点评：本题考查了同一坐标系中指数函数图象与二次函数图象的关系，根据指数函数图象确定出a、b的正负情况是求解的关键．
练习册系列答案
相关题目
设集合M={x|x2-2x-3＜0}，N={x|log2（1-x）＜1}，则M∩∁RN等于（ ）
| A、[-1，1] |
| B、（-1，0） |
| C、[1，3） |
| D、（0，1） |
已知函数f（x）=x2+2a1og2（x2+2）+a2-3有且只有一个零点，则实数a的值为（ ）
| A、1 | B、-3 | C、2 | D、1或-3 |
复数z=
（i为虚数单位且a＜0）在复平面内对应的点位于（ ）
| 3-ai |
| i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
若向量
=（2，-1），
=（0，2），则以下向量中与
+
垂直的是（ ）
| a |
| b |
| a |
| b |
| A、（1，-2） |
| B、（1，2） |
| C、（2，1） |
| D、（0，2） |
若复数z满足：z+|z|=1+2i，则z的虚部为（ ）
| A、2i | B、1 | C、2 | D、i |
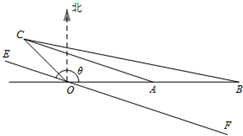如图，O为总信号源点，A，B，C是三个居民区，已知A，B都在O的正东方向上，OA=10km，OB=20km，C在O的北偏西45°方向上，CO=5