题目内容
在△ABC中,设角A,B,C的对边分别为a,b,c,满足A=B+30°.
(1)若c=1,b=sinB,求B.
(2)若a2+c2-
ac=b2,求sinA的值.
(1)若c=1,b=sinB,求B.
(2)若a2+c2-
| 1 |
| 2 |
考点:正弦定理,余弦定理
专题:三角函数的求值,解三角形
分析:(1)利用正弦定理和已知条件求得sinC的值,进而求得C,然后利用内角和和已知A,B的关系求得B.
(2)利用余弦定理与已知等式求得cosB,进而求得sinB,利用两角和公式求得sin(B+
)的值,进而求得sinA.
(2)利用余弦定理与已知等式求得cosB,进而求得sinB,利用两角和公式求得sin(B+
| π |
| 6 |
解答:
解:(1)∵
=
,
∴sinC=
•sinB=1,
∵0<C<π,
∴C=
,则A+B=
,
∵A=B+30°,
∴B=
.
(2)∵a2+c2-
ac=b2,
∴cosB=
=
,
∵0<B<π,
∴sinB=
=
,
∴sinA=sin(B+
)=
sinB+
cosB=
×
+
×
=
.
| c |
| sinC |
| b |
| sinB |
∴sinC=
| c |
| b |
∵0<C<π,
∴C=
| π |
| 2 |
| π |
| 2 |
∵A=B+30°,
∴B=
| π |
| 6 |
(2)∵a2+c2-
| 1 |
| 2 |
∴cosB=
| a2+c2-b2 |
| 2ac |
| 1 |
| 4 |
∵0<B<π,
∴sinB=
| 1-cos2B |
| ||
| 4 |
∴sinA=sin(B+
| π |
| 6 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
3
| ||
| 8 |
点评:本题主要考查了正弦定理和余弦定理的应用.考查了学生正弦定理和余弦定理公式的熟练运用.

练习册系列答案
相关题目
若复数z满足:z+|z|=1+2i,则z的虚部为( )
| A、2i | B、1 | C、2 | D、i |
 如图,已知
如图,已知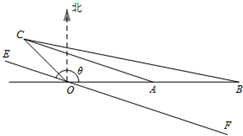 如图,O为总信号源点,A,B,C是三个居民区,已知A,B都在O的正东方向上,OA=10km,OB=20km,C在O的北偏西45°方向上,CO=5
如图,O为总信号源点,A,B,C是三个居民区,已知A,B都在O的正东方向上,OA=10km,OB=20km,C在O的北偏西45°方向上,CO=5