题目内容
某商品进价每个80元，零售价每个100元，为促进销售，拟采用买一件商品赠送顾客一件价值1元的小礼品的方法，结果在单位销售周期内销量增加10%，实践表明，在一定范围内，礼品价值为（n+1）元（n∈N）时比礼品价值为n元时销售量增加10%，请你为商品设计礼品价值，以求最大利润．
考点：函数模型的选择与应用
专题：应用题,等差数列与等比数列
分析：根据等比数列模型写出商场销售电扇所得利润an的表达式，比较数列的前一项和后一项的大小，进行作商比较，即可求出相应的n的值．
解答：
解：设未赠礼品，销量为1，an为当礼品价值为n（n∈N*）元时，商场销售电扇所得利润，则
an=1.1n（20-n）（1≤n≤20，n∈N*），
∴
=1.1×
∴当n≤9时，an+1≥an；当n≥9时，an+1≤an．
∴当n=9时，利润最大．
an=1.1n（20-n）（1≤n≤20，n∈N*），
∴
| an+1 |
| an |
| 19-n |
| 20-n |
∴当n≤9时，an+1≥an；当n≥9时，an+1≤an．
∴当n=9时，利润最大．
点评：本题主要考查了等比数列的应用，同时考查了研究数列的最值问题，属于中档题．
练习册系列答案
相关题目
已知集合A={x|x2-1＜0}，B={x|x＜m}，若“a∈A”是“a∈B”的充分而不必要条件，则实数m的取值可以是（ ）
A、
| ||
B、
| ||
| C、1 | ||
D、
|
已知函数f（x）=x2+2a1og2（x2+2）+a2-3有且只有一个零点，则实数a的值为（ ）
| A、1 | B、-3 | C、2 | D、1或-3 |
若向量
=（2，-1），
=（0，2），则以下向量中与
+
垂直的是（ ）
| a |
| b |
| a |
| b |
| A、（1，-2） |
| B、（1，2） |
| C、（2，1） |
| D、（0，2） |
若复数z满足：z+|z|=1+2i，则z的虚部为（ ）
| A、2i | B、1 | C、2 | D、i |
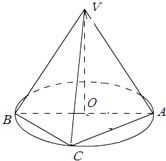如图，AB是圆O的直径，点C是弧AB的中点，点V是圆O所在平面外一点，已知AB=2，VA=VB=VC=2．