题目内容
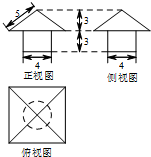
某三棱锥的三视图如图所示,则其表面中,直角三角形的个数为( )


| A、1个 | B、2个 | C、3个 | D、4个 |
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:结合直观图判断三棱锥的最里面的侧面与底面垂直,底面△ABC为直角三角形,侧面△SAC为直角三角形,再通过证明BC⊥平面SAC,证明△SBC为直角三角形;
通过证明SA⊥平面SBC,证明△SAB为直角三角形,由此可得答案.
通过证明SA⊥平面SBC,证明△SAB为直角三角形,由此可得答案.
解答:
解:由三视图知三棱锥的最里面的侧面与底面垂直,如图:

底面△ABC为直角三角形,侧面△SAC为直角三角形,
∵平面SAC⊥平面ABC,BC⊥AC,∴BC⊥平面SAC,∴BC⊥SC,∴△SBC为直角三角形;
又SA⊥SC,SA⊥BC,∴SA⊥平面SBC,∴SA⊥SB,∴△SAB为直角三角形.
故选:D.

底面△ABC为直角三角形,侧面△SAC为直角三角形,
∵平面SAC⊥平面ABC,BC⊥AC,∴BC⊥平面SAC,∴BC⊥SC,∴△SBC为直角三角形;
又SA⊥SC,SA⊥BC,∴SA⊥平面SBC,∴SA⊥SB,∴△SAB为直角三角形.
故选:D.
点评:本题考查了由三视图判断几何体的特征,考查了学生的推理论证能力,根据三视图判断几何体的线面、线线、面面关系是关键.

练习册系列答案
相关题目
如图所示是某一几何体的三视图,则它的体积为( )

| A、16+12π |
| B、48+12π |
| C、64+12π |
| D、64+16π |
在平行四边形ABCD中,
=
,
=
,
=3
,M为BC的中点,则
=( )
| AB |
| a |
| AD |
| b |
| AN |
| NC |
| MN |
A、-
| ||||||||
B、-
| ||||||||
C、
| ||||||||
D、-
|
设f(x)=ax2+bx+c(a,b,c∈R),e为自然对数的底数.若f′(x)lnx>
.则( )
| f(x) |
| x |
| A、f(2)<f(e)ln2,2f(e)>f(e2) |
| B、f(2)<f(e)ln2,2f(e)<f(e2) |
| C、f(2)>f(e)ln2,2f(e)<f(e2) |
| D、f(2)>f(e)ln2,2f(e)>f(e2) |
设全集U={3,4,5,6},集合A={3,5,6},B={4,5,6},则∁UA∩B=( )
| A、{4,7} | B、{3,6} |
| C、{4} | D、{7} |
若曲线y=x2+ax+b在点(1,b)处的切线方程是x-y+1=0,则( )
| A、a=1,b=2 |
| B、a=-1,b=2 |
| C、a=1,b=-2 |
| D、a=-1,b=-2 |
下列命题中的真命题是( )
| A、?x∈R,x2>0 | ||
B、?x∈R,x+
| ||
| C、?x0∈R,sinx0+cosx0=2 | ||
D、?x0∈R,ln x0>(
|