题目内容
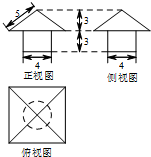
如图所示是某一几何体的三视图，则它的体积为（ ）
| A、16+12π |
| B、48+12π |
| C、64+12π |
| D、64+16π |
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：几何体是圆柱与正四棱锥的组合体，根据三视图判断圆柱的高与底面半径，判断正四棱锥的高及侧面上的斜高，求出正四棱锥的底面边长，把数据代入圆柱与棱锥的体积公式计算．
解答：
解：由三视图知：几何体是圆柱与正四棱锥的组合体，
圆柱的高为3，底面直径为4，∴圆柱的体积为π×22×3=12π；
正四棱锥的高为3，侧面上的斜高为5，∴正四棱锥的底面边长为2
=8，
∴四棱锥的体积为
×82×3=64．
故几何体的体积V=64+12π．
故选：C．
圆柱的高为3，底面直径为4，∴圆柱的体积为π×22×3=12π；
正四棱锥的高为3，侧面上的斜高为5，∴正四棱锥的底面边长为2
| 52-32 |
∴四棱锥的体积为
| 1 |
| 3 |
故几何体的体积V=64+12π．
故选：C．
点评：本题考查了由三视图求几何体的体积，根据三视图判断几何体的形状及数据所对应的几何量是关键．
练习册系列答案
阅读快车系列答案
相关题目
定积分
（-3）dx等于（ ）
| ∫ | 3 1 |
| A、-6 | B、6 | C、-3 | D、3 |
已知a=0.3-0.2，b=log0.50.8，c=log0.53，那么a，b，c的大小关系是（ ）
| A、a＜b＜c |
| B、c＜b＜a |
| C、c＜a＜b |
| D、a＜c＜b |
一观览车的主架示意图如图所示，其中O为轮轴的中心，距地面32m（即OM长），巨轮的半径为30m，AM=BP=2m，巨轮逆时针旋转且每12分钟转动一圈．若点M为吊舱P的初始位置，经过t分钟，该吊舱P距离地面的高度为h（t）m，则h（t）=（ ）A、30sin（
| ||||
B、30sin（
| ||||
C、30sin（
| ||||
D、30sin（
|
下列函数中，既是偶函数又在（-∞，0）上单调递增的是（ ）
| A、y=x2 | ||
| B、y=2|x| | ||
C、y=log2
| ||
| D、y=sinx |
某三棱锥的三视图如图所示，则其表面中，直角三角形的个数为（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜