题目内容
已知f（x）是二次函数，关于x的方程mf2（x）+nf（x）+p=0（m，n，p都是实数）有四个不同的实数根，且它们从小到大的顺序为：x1＜x2＜x3＜x4，则x1-x2-x3+x4的值为 ．
考点：等比数列的性质
专题：等差数列与等比数列
分析：由于关于x的方程mf2（x）+nf（x）+p=0（m，n，p都是实数）有四个不同的实数根，可得上述因此方程的解必是f（x）=k1，f（x）=k2的形式．设k1＞k2，可得f（x）=k1的解为x1，x4；f（x）=k2的解为x2，x3，再利用根与系数的关系即可得出．
解答：
解：∵关于x的方程mf2（x）+nf（x）+p=0（m，n，p都是实数）有四个不同的实数根，
∴m≠0，△＞0，
上述因此方程的解必是f（x）=k1，f（x）=k2的形式．
设k1＞k2，则f（x）=k1的解为x1，x4；f（x）=k2的解为x2，x3，且x1+x4=x2+x3．
∴x1-x2-x3+x4=0．
故答案为：0．
∴m≠0，△＞0，
上述因此方程的解必是f（x）=k1，f（x）=k2的形式．
设k1＞k2，则f（x）=k1的解为x1，x4；f（x）=k2的解为x2，x3，且x1+x4=x2+x3．
∴x1-x2-x3+x4=0．
故答案为：0．
点评：本题考查了等价问题的转化、一元二次方程的根与系数，考查了推理能力，属于难题．
练习册系列答案
名校课堂系列答案
相关题目
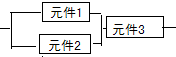某一部件由三个电子元件按如图所示方式连接而成，元件1或元件2正常工作，则部件正常工作：设三个电子元件的使用寿命（单位：小时）均服从正态分布N（1000，σ2），若每个元件使用寿命超过1200小时的概率为定积分
（-3）dx等于（ ）
| ∫ | 3 1 |
| A、-6 | B、6 | C、-3 | D、3 |
某三棱锥的三视图如图所示，则其表面中，直角三角形的个数为（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |