题目内容
任意一个三位数，百位数与个位数相加等于十位数，求证：该三位数能被11整除．
考点：整除的基本性质
专题：证明题
分析：不妨设这个三位数为xyz，结合已知可得x+z=y，除以11后，可得结论．
解答：
证明：设这个三位数A的三个数位上数依次为xyz，
则x+z=y，
则A=100x+10y+z=100x+10（x+z）+z=110x+11z，
则A÷11=10x+z，
即该三位数能被11整除．
则x+z=y，
则A=100x+10y+z=100x+10（x+z）+z=110x+11z，
则A÷11=10x+z，
即该三位数能被11整除．
点评：此题考查了数的整除特征，明确能被11整除的数的特征：即该数的奇数位和与偶数位和之间的差是11的倍数，是解答此题的关键．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
已知圆C：（x-a）2+（y-2）2=4（a＞0）及直线l：x-y+3=0．当直线l被圆C截得的弦长为2
时，则a的值为（ ）
| 2 |
| A、1 | B、1或3 |
| C、-3 | D、1或-3 |
二项式（2x2-
）6的展开式中第4项的系数是（ ）
| 1 | |||
|
| A、20 | B、60 |
| C、-160 | D、160 |
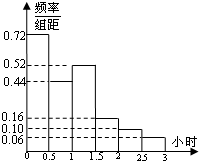电视传媒为了解某市100万观众对足球节目的收视情况，随机抽取了100名观众进行调查．如图是根据调查结果绘制的观众每周平均收看足球节目时间的频率分布直方图，将每周平均收看足球节目时间不低于1.5小时的观众称为“足球迷”，并将其中每周平均收看足球节目时间不低于2.5小时的观众称为“铁杆足球迷”．
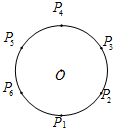如图，设P1，P2，…，P6为单位圆上逆时针均匀分布的六个点．现从这六个点中任选其中三个不同点构成一个三角形，记该三角形的面积为随机变量S．