题目内容
已知函数f(x)=lnx-
ax2+bx(a>0)且f′(1)=0
(1)试用含有a的式子表示b;
(2)若a=1,求函数f(x)的单调区间;
(3)对于曲线上的不同两点P1(x1,y1),P2(x2,y2),如果存在曲线上的点Q(x0,y0)且x1<x0<x2,使得曲线在点Q处的切线l∥P1P2,则称P1P2存在“陪伴切线”.特别地,当x0=
时,又称P1P2存在“中值陪伴切线”.试问:在函数f(x)上是否存在两点P1,P2使得它存在“中值陪伴切线”?若存在,求出P1,P2的坐标,若不存在,请说明理由.
| 1 |
| 2 |
(1)试用含有a的式子表示b;
(2)若a=1,求函数f(x)的单调区间;
(3)对于曲线上的不同两点P1(x1,y1),P2(x2,y2),如果存在曲线上的点Q(x0,y0)且x1<x0<x2,使得曲线在点Q处的切线l∥P1P2,则称P1P2存在“陪伴切线”.特别地,当x0=
| x1+x2 |
| 2 |
考点:导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(1)利用导数解决,由f′(1)=0即得;
(2)利用导数求得函数的单调区间即可;
(3)假设k=f′(x0),则得ln
=
,令t=
,则u(t)=lnt-
(0<t<1),
利用导数求得u(t)<u(1)=0,假设k=f′(x0)不成立,故得出结论.
(2)利用导数求得函数的单调区间即可;
(3)假设k=f′(x0),则得ln
| x1 |
| x2 |
2
| ||
|
| x1 |
| x2 |
| 2t-2 |
| t+1 |
利用导数求得u(t)<u(1)=0,假设k=f′(x0)不成立,故得出结论.
解答:
解:(1)f(x)的定义域为(0,+∞),
∵函数f(x)=lnx-
ax2+bx(a>0)
∴f′(x)=
-ax+b,又∵f′(1)=0
∴b=a-1.
(2)由a=1得,b=0,∴f′(x)=
-x=
,
∴由f′(x)>0得,0<x<1;由f′(x)<0得,x>1;
∴f(x)的单调增区间是(0,1),单调减区间是(1,+∞).
(3)因P1、P2在f(x)=lnx-
ax2+bx(a>0)的图象上,
∴y1=lnx1-
a
+(a-1)x1,y2=lnx2-
a
+(a-1)x2,
∴k=
=
-
a(x2+x1)+a-1,
∵x0=
,
∴f′(x)=
-ax+a-1
∴f′(x0)=
-a•
+a-1,
假设k=f′(x0),则得:
-
a(x2+x1)+a-1)=
-a•
+a-1,
即
=
,即ln
=
令t=
,则u(t)=lnt-
(0<t<1),
∵u′(t)=
>0,
∴u(t)在(0,1)上是增函数,∴u(t)<u(1)=0,
∴lnt-
<0,∴假设k=f′(x0)不成立,故假设k≠f′(x0).
∵函数f(x)=lnx-
| 1 |
| 2 |
∴f′(x)=
| 1 |
| x |
∴b=a-1.
(2)由a=1得,b=0,∴f′(x)=
| 1 |
| x |
| (1-x)(1+x) |
| x |
∴由f′(x)>0得,0<x<1;由f′(x)<0得,x>1;
∴f(x)的单调增区间是(0,1),单调减区间是(1,+∞).
(3)因P1、P2在f(x)=lnx-
| 1 |
| 2 |
∴y1=lnx1-
| 1 |
| 2 |
| x | 2 1 |
| 1 |
| 2 |
| x | 2 2 |
∴k=
| y2-y1 |
| x2-x1 |
| lnx2-lnx1 |
| x2-x1 |
| 1 |
| 2 |
∵x0=
| x2+x1 |
| 2 |
∴f′(x)=
| 1 |
| x |
∴f′(x0)=
| 2 |
| x2+x1 |
| x2+x1 |
| 2 |
假设k=f′(x0),则得:
| lnx2-lnx1 |
| x2-x1 |
| 1 |
| 2 |
| 2 |
| x2+x1 |
| x2+x1 |
| 2 |
即
| lnx2-lnx1 |
| x2-x1 |
| 2 |
| x2+x1 |
| x1 |
| x2 |
2
| ||
|
令t=
| x1 |
| x2 |
| 2t-2 |
| t+1 |
∵u′(t)=
| (t-1)2 |
| t(t+1)2 |
∴u(t)在(0,1)上是增函数,∴u(t)<u(1)=0,
∴lnt-
| 2t-2 |
| t+1 |
点评:本题主要考查利用导数研究判断函数的单调性及求函数的单调区间最值等知识,考查解决存在性问题的转化策略,属难题.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
已知sin(θ+π)<0,cos(θ-π)>0,则θ是第( )象限角.
| A、一 | B、二 | C、三 | D、四 |
若实数x,y满足不等式组
,则y-3x的最大值为( )
|
| A、-6 | B、-3 | C、-2 | D、-1 |
曲线f(x)=ex(其中e为自然对数的底数)在点(0,1)处的切线与直线y=-x+3和x轴所围成的区域D(包含边界),点P(x,y)为区域D内的动点,则z=x-3y的最大值为( )
| A、3 | B、4 | C、-1 | D、2 |
 如图,是2008年底CCTV举办的全国钢琴、小提琴大赛比赛现场上七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据方差为
如图,是2008年底CCTV举办的全国钢琴、小提琴大赛比赛现场上七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据方差为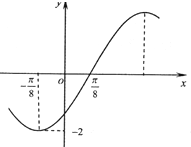 已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<
已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<