题目内容
已知函数f(x)的定义域为D,若它的值域是D的子集,则称f(x)在D上封闭.
(Ⅰ)试判断f(x)=2x,g(x)=log2x是否在(1,+∞)上封闭;
(Ⅱ)设f1(x)=f(x),fn(x)=f(fn-1(x))(n∈N*,n≥2),若fn(x)(n∈N*)的定义域均为D,求证:fn(x)在D上封闭的充分必要条件是f1(x)在D上封闭;
(Ⅲ)若a>0,求证:h(x)=
(|xsinx|+|xcosx|)在[0,a]上封闭,并指出值域为[0,a]时a的值.
(Ⅰ)试判断f(x)=2x,g(x)=log2x是否在(1,+∞)上封闭;
(Ⅱ)设f1(x)=f(x),fn(x)=f(fn-1(x))(n∈N*,n≥2),若fn(x)(n∈N*)的定义域均为D,求证:fn(x)在D上封闭的充分必要条件是f1(x)在D上封闭;
(Ⅲ)若a>0,求证:h(x)=
| ||
| 2 |
考点:利用导数研究曲线上某点切线方程
专题:新定义,函数的性质及应用
分析:(Ⅰ)根据函数封闭的定义封闭求出两个函数的值域即可判断f(x)=2x,g(x)=log2x是否在(1,+∞)上封闭;
(Ⅱ)根据封闭的定义,即可证明fn(x)在D上封闭的充分条件是f1(x)在D上封闭,利用反证法即可证明fn(x)在D上封闭的必要条件是f1(x)在D上封闭;
(Ⅲ)求出|sinx|+|cosx|的取值范围为[1,
],由0≤x≤a,推出0≤h(x)≤a,即封闭,由|sina|+|cosa|=
,推出a=
+kπ(k∈N).
(Ⅱ)根据封闭的定义,即可证明fn(x)在D上封闭的充分条件是f1(x)在D上封闭,利用反证法即可证明fn(x)在D上封闭的必要条件是f1(x)在D上封闭;
(Ⅲ)求出|sinx|+|cosx|的取值范围为[1,
| 2 |
| 2 |
| π |
| 4 |
解答:
解:(Ⅰ)当x>1时,f(x)=2x∈(2,+∞),f(x)在(1,+∞)上封闭,
g(x)=log2x∈(0,+∞),g(x)在(1,+∞)上不封闭;
(Ⅱ)证明:设f1(x)=f(x),fn(x)=f(fn-1(x))(n∈N*,n≥2),
先证:fn(x)在D上封闭的充分条件是f1(x)在D上封闭,
任取x∈D,∵f1(x)在D上封闭,∴f2(x)=f(f1(x))∈D,…,fn(x)=f(fn-1(x)))∈D,
∴fn(x)在D上封闭的充分条件是f1(x)在D上封闭;
再证:fn(x)在D上封闭的必要条件是f1(x)在D上封闭.
考虑运用反证法,假设f1(x)在D上不封闭,即存在x0∈D,使得f(x0)∉D,
那么f2(x0)=f(f1(x0))无意义,这与fn(x)(n∈N*)的定义域均为D矛盾,故假设不成立,
即f1(x)在D上封闭是fn(x)在D上封闭的必要条件.
故fn(x)在D上封闭的充分必要条件是f1(x)在D上封闭;
(Ⅲ)证明:∵a>0,0≤x≤a,
∴h(x)=
(|xsinx|+|xcosx|)=
x(|sinx|+|cosx|),
∵|sinx|+|cosx|=
=
∈[1,
],
∴0≤h(x)≤
•a•
=a,
∴h(x)在[0,a]上封闭;
若值域为[0,a],由上面可知,|sinx|+|cosx|=
,
则h(x)≤
•x•
=x≤a,
即|sina|+|cosa|=
,
∴a=
+kπ(k∈N).
g(x)=log2x∈(0,+∞),g(x)在(1,+∞)上不封闭;
(Ⅱ)证明:设f1(x)=f(x),fn(x)=f(fn-1(x))(n∈N*,n≥2),
先证:fn(x)在D上封闭的充分条件是f1(x)在D上封闭,
任取x∈D,∵f1(x)在D上封闭,∴f2(x)=f(f1(x))∈D,…,fn(x)=f(fn-1(x)))∈D,
∴fn(x)在D上封闭的充分条件是f1(x)在D上封闭;
再证:fn(x)在D上封闭的必要条件是f1(x)在D上封闭.
考虑运用反证法,假设f1(x)在D上不封闭,即存在x0∈D,使得f(x0)∉D,
那么f2(x0)=f(f1(x0))无意义,这与fn(x)(n∈N*)的定义域均为D矛盾,故假设不成立,
即f1(x)在D上封闭是fn(x)在D上封闭的必要条件.
故fn(x)在D上封闭的充分必要条件是f1(x)在D上封闭;
(Ⅲ)证明:∵a>0,0≤x≤a,
∴h(x)=
| ||
| 2 |
| ||
| 2 |
∵|sinx|+|cosx|=
| sin2x+cos2x+|sin2x| |
| 1+|sin2x| |
| 2 |
∴0≤h(x)≤
| ||
| 2 |
| 2 |
∴h(x)在[0,a]上封闭;
若值域为[0,a],由上面可知,|sinx|+|cosx|=
| 2 |
则h(x)≤
| ||
| 2 |
| 2 |
即|sina|+|cosa|=
| 2 |
∴a=
| π |
| 4 |
点评:本题主要考查函数值域的求法,以及与函数有关的新定义,利用反证法是解决本题的关键,综合性较强

练习册系列答案
相关题目
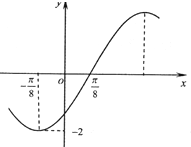 已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<
已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<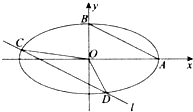 如图,A、B是椭圆
如图,A、B是椭圆