题目内容
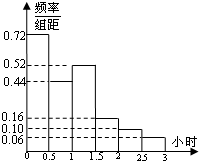 电视传媒为了解某市100万观众对足球节目的收视情况,随机抽取了100名观众进行调查.如图是根据调查结果绘制的观众每周平均收看足球节目时间的频率分布直方图,将每周平均收看足球节目时间不低于1.5小时的观众称为“足球迷”,并将其中每周平均收看足球节目时间不低于2.5小时的观众称为“铁杆足球迷”.
电视传媒为了解某市100万观众对足球节目的收视情况,随机抽取了100名观众进行调查.如图是根据调查结果绘制的观众每周平均收看足球节目时间的频率分布直方图,将每周平均收看足球节目时间不低于1.5小时的观众称为“足球迷”,并将其中每周平均收看足球节目时间不低于2.5小时的观众称为“铁杆足球迷”.(1)试估算该市“足球迷”的人数,并指出其中“铁杆足球迷”约为多少人;
(2)该市要举办一场足球比赛,已知该市的足球场可容纳10万名观众.根据调查,如果票价定为100元/张,则非“足球迷”均不会到现场观看,而“足球迷”均愿意前往现场观看.如果票价提高10x元/张(x∈N),则“足球迷”中非“铁杆足球迷”愿意前往观看的人数会减少10x%,“铁杆足球迷”愿意前往观看的人数会减少
| 100x |
| x+11 |
考点:频率分布直方图
专题:不等式的解法及应用,概率与统计
分析:(1)求出后三组数据的频率之和,利用频率乘以样本容量得频数求得“足球迷”的人数和“铁杆足球迷”人数;
(2)设票价为100+10x元,求出一般“足球迷”和“铁杆足球迷”中去现场看球的人数,根据现场观看足球比赛的人数不超过10万人,列出不等式.通过解不等式求得正整数x的值,可得答案.
(2)设票价为100+10x元,求出一般“足球迷”和“铁杆足球迷”中去现场看球的人数,根据现场观看足球比赛的人数不超过10万人,列出不等式.通过解不等式求得正整数x的值,可得答案.
解答:
解:(1)样本中“足球迷”出现的频率=(0.16+0.10+0.06)×0.5=16%,
“足球迷”的人数=100×16%=16(万),
“铁杆足球迷”=100×(0.06×0.5)=3(万)
∴16万“足球迷”中,“铁杆足球迷”约有3万人;
(2)设票价为100+10x元,则一般“足球迷”中约有13(1-10x%)万人,
“铁杆足球迷”约有3(1-
%)万人去现场看球,
令13(1-10x%)+3(1-
%)=16-
-
≤10,
化简得:13x2+113x-660≥0
解得:x≤-
,或x≥4,由x∈N,∴x≥4,
即平均票价至少定为100+40=140元,才能使前往现场观看足球比赛的“足球迷”不超过10万人.
“足球迷”的人数=100×16%=16(万),
“铁杆足球迷”=100×(0.06×0.5)=3(万)
∴16万“足球迷”中,“铁杆足球迷”约有3万人;
(2)设票价为100+10x元,则一般“足球迷”中约有13(1-10x%)万人,
“铁杆足球迷”约有3(1-
| 100x |
| x+11 |
令13(1-10x%)+3(1-
| 100x |
| x+11 |
| 13x |
| 10 |
| 3x |
| x+11 |
化简得:13x2+113x-660≥0
解得:x≤-
| 165 |
| 13 |
即平均票价至少定为100+40=140元,才能使前往现场观看足球比赛的“足球迷”不超过10万人.
点评:本题考查了由频率分布直方图求频率与频数,考查了不等式的实际应用,列出关于票价x的不等式是解答本题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
执行如图所示的程序框图.若输入x=3,则输出k的值是( )


| A、3 | B、4 | C、5 | D、6 |
若实数x,y满足不等式组
,则y-3x的最大值为( )
|
| A、-6 | B、-3 | C、-2 | D、-1 |
 如图,A、B是椭圆
如图,A、B是椭圆