题目内容
11.已知圆C:(x-3)2+(y-4)2=4,直线l过定点A(1,0).(1)若l与圆C相切,求l的方程;
(2)若l与圆C相交于P,Q两点,求△CPQ的面积的最大值,并求此时直线l的方程.(其中点C是圆的圆心)
分析 (1)直线l无斜率时,直线l的方程为x=1,成立;直线l有斜率时,设方程为kx-y-k=0,由圆心到直线的距离等于半径,能求出直线l的方程.
(2)△CPQ面积最大时,△CPQ是等腰直角三角形,此时圆心到直线的距离为$\sqrt{2}$,设直线l的方程为kx-y-k=0,由此能求出直线l的方程.
解答 解:(1)直线l无斜率时,直线l的方程为x=1,
此时直线l和圆C相切.
直线l有斜率时,设方程为y=k(x-1),即kx-y-k=0,
∵l与圆C相切,∴圆心到直线的距离等于半径,
即$d=\frac{{|{3k-4-k}|}}{{\sqrt{{k^2}+1}}}=2$,
解得k=$\frac{3}{4}$,∴直线l的方程为$y=\frac{3}{4}x-\frac{3}{4}$
(2)△CPQ面积最大时,∠PCQ=90°,$S=\frac{1}{2}×2×2=2$,
即△CPQ是等腰直角三角形,
由半径r=2得:圆心到直线的距离为$\sqrt{2}$
设直线l的方程为:y=k(x-1),即kx-y-k=0,
则$d=\frac{{|{2k-4}|}}{{\sqrt{{k^2}+1}}}=\sqrt{2}$,∴k=7或k=1,
∴直线l的方程为:y=7x-7,y=x-1.
点评 本题考查直线方程的求法、直线与椭圆位置关系,本题突出对运算能力、化归转化能力的考查,是中档题,解题时要认真审题,注意点到直线的距离公式的合理运用.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
18.将一个底面半径为1,高为2的圆锥形工件切割成一个圆柱体,能切割出的圆柱最大体积为( )
| A. | $\frac{π}{27}$ | B. | $\frac{8π}{27}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{9}$ |
19.设Sn是等差数列{an}的前n项和,且a11=S13=13,则a9=( )
| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
3.在复平面内,复数$\frac{2-i}{1-i}$(i是虚数单位)对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
20.下列命题中正确的是( )
| A. | 若p∨q为真命题,则p∧q为真命题 | |
| B. | “x=5”是“x2-4x-5=0”的充分不必要条件 | |
| C. | 命题“若x<-1,则x2-2x-3>0”的否命题为:“若x<-1,则x2-2x-3≤0” | |
| D. | 已知命题p:?x∈R,x2+x-1<0,则¬p:?x∈R,x2+x-1≥0 |
1.已知曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的渐近线方程为y=±$\frac{\sqrt{2}}{2}$x,则该曲线的离心率为( )
| A. | $\frac{\sqrt{6}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\sqrt{3}$ |
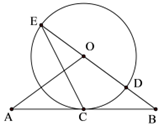 如图,直线AB经过⊙O上一点C,且OA=OB,CA=CB,⊙O交直线OB于E、D.
如图,直线AB经过⊙O上一点C,且OA=OB,CA=CB,⊙O交直线OB于E、D.