题目内容
19．设Sn是等差数列{an}的前n项和，且a11=S13=13，则a9=（ ）| A． | 9 | B． | 8 | C． | 7 | D． | 6 |
分析 利用等差数列的通项公式与求和公式即可得出．
解答 解：设等差数列{an}的公差为d，∵a11=S13=13，∴a1+10d=13a1+$\frac{13×12}{2}$d=13，
解得a1=-17，d=3．
则a9=-17+8×3=7．
故选：C．
点评 本题考查了等差数列的通项公式与求和公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
6．已知直角梯形ABCD中，AB∥CD，AB⊥AD，AB=4，CD=6，AD=5，点E在梯形内，那么∠AEB为钝角的概率为（ ）
| A． | $\frac{2π}{25}$ | B． | $\frac{4π}{25}$ | C． | $\frac{1}{2}$ | D． | $\frac{1}{4}$ |
7．
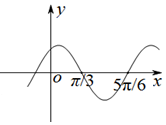已知函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜π）的图象如图所示，将f（x）的图象向左平移$\frac{π}{6}$个单位，得到g（x）的图象，则函数g（x）的解析式为（ ）
已知函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜π）的图象如图所示，将f（x）的图象向左平移$\frac{π}{6}$个单位，得到g（x）的图象，则函数g（x）的解析式为（ ）| A． | g（x）=sin2x | B． | g（x）=cos2x | C． | $g（x）=sin（2x+\frac{π}{6}）$ | D． | $g（x）=sin（2x+\frac{2π}{3}）$ |
8．已知复数$z=\frac{2+ai}{3-i}$是纯虚数（其中i为虚数单位，a∈R），则z的虚部为（ ）
| A． | 2 | B． | -2 | C． | 2i | D． | -2i |
9．
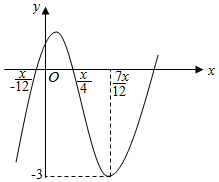已知函数f（x）=Asin（ωx+φ）+B（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，将函数f（x）的图象向左平移m（m＞0）个单位后，得到的图象关于点（$\frac{π}{6}$，-1）对称，则m的最小值是（ ）
已知函数f（x）=Asin（ωx+φ）+B（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，将函数f（x）的图象向左平移m（m＞0）个单位后，得到的图象关于点（$\frac{π}{6}$，-1）对称，则m的最小值是（ ）| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{5}{6}$π | D． | $\frac{2π}{3}$ |