题目内容
2．已知等差数列{bn}和各项都是正数的数列{an}，且a1=b1=1，b2+b4=10，满足an2-2anan+1+an-2an+1=0（1）求{an}和{bn}通项公式；
（2）设cn=$\frac{1}{a_n}+{b_n}$，求数列{cn}的前n项和．
分析 （1）由已知得到等差数列{bn}的公差的方程解之；结合an2-2anan+1+an-2an+1=0，得到（an+1）an=2an+1（an+1），数列{an}是以1为首项$\frac{1}{2}$为公比的等比数列，得到通项公式．
（2）首项得到数列{cn}的通项公式，利用错位相减法求和．
解答 解：（1）因为等差数列{bn}a1=b1=1，b2+b4=10，满足an2-2anan+1+an-2an+1=0，
所以2b1+4d=10，解得d=2，所以bn=2n-1；
由an2-2anan+1+an-2an+1=0，得到（an+1）an=2an+1（an+1），
数列{an}各项都是正数，所以$\frac{{a}_{n+1}}{{a}_{n}}=\frac{1}{2}$，
所以数列{an}是以1为首项$\frac{1}{2}$为公比的等比数列，所以an=$\frac{1}{{2}^{n-1}}$．
（2）设cn=$\frac{1}{a_n}+{b_n}$=2n-1+2n-1，
所以数列{cn}的前n项和${S}_{n}=（{2}^{0}+{2}^{1}+{2}^{2}+…+{2}^{n-1}）$+2（1+2+3+…+n）-n
=$\frac{1-{2}^{n}}{1-2}+2×\frac{n（n+1）}{2}-n$=2n+n2-1．
点评 本题考查了等差数列和等比数列通项公式的求法以及利用错位相减法对数列求和；属于经常考查题型．
练习册系列答案
相关题目
9．四个变量y1、y2、y3、y4随变量x变化的函数值如表：
关于x呈单调增加的指数型函数和线性函数变化的变量分别是（ ）
| x | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| y1 | 5 | 130 | 505 | 1130 | 2005 | 3130 | 4505 |
| y2 | 5 | 94.478 | 1785.2 | 33733 | 6.37×105 | 1.2×107 | 2.28×108 |
| y3 | 5 | 30 | 55 | 80 | 105 | 130 | 155 |
| y4 | 5 | 2.3107 | 1.4295 | 1.1407 | 1.0461 | 1.0151 | 1.005 |
| A． | y2、y1 | B． | y2、y3 | C． | y4、y3 | D． | y1、y3 |
7．
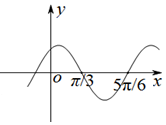已知函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜π）的图象如图所示，将f（x）的图象向左平移$\frac{π}{6}$个单位，得到g（x）的图象，则函数g（x）的解析式为（ ）
已知函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜π）的图象如图所示，将f（x）的图象向左平移$\frac{π}{6}$个单位，得到g（x）的图象，则函数g（x）的解析式为（ ）| A． | g（x）=sin2x | B． | g（x）=cos2x | C． | $g（x）=sin（2x+\frac{π}{6}）$ | D． | $g（x）=sin（2x+\frac{2π}{3}）$ |