题目内容
1.已知曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的渐近线方程为y=±$\frac{\sqrt{2}}{2}$x,则该曲线的离心率为( )| A. | $\frac{\sqrt{6}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\sqrt{3}$ |
分析 利用双曲线的渐近线方程,推出a,b关系然后求解双曲线的离心率即可.
解答 解:双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的渐近线方程为y=±$\frac{\sqrt{2}}{2}$x,
可得$\frac{b}{a}$=$\frac{\sqrt{2}}{2}$,即$\frac{{c}^{2}-{a}^{2}}{{a}^{2}}=\frac{1}{2}$,可得e=$\frac{\sqrt{6}}{2}$.
故选:A.
点评 本题考查双曲线的简单性质的应用,渐近线方程的应用,离心率的求法,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.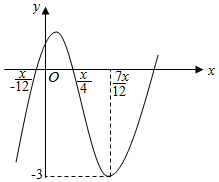 已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,将函数f(x)的图象向左平移m(m>0)个单位后,得到的图象关于点($\frac{π}{6}$,-1)对称,则m的最小值是( )
已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,将函数f(x)的图象向左平移m(m>0)个单位后,得到的图象关于点($\frac{π}{6}$,-1)对称,则m的最小值是( )
 已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,将函数f(x)的图象向左平移m(m>0)个单位后,得到的图象关于点($\frac{π}{6}$,-1)对称,则m的最小值是( )
已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,将函数f(x)的图象向左平移m(m>0)个单位后,得到的图象关于点($\frac{π}{6}$,-1)对称,则m的最小值是( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{5}{6}$π | D. | $\frac{2π}{3}$ |
10.阅读如图的程序框图,运行相应的程序,则输出s的值为( )
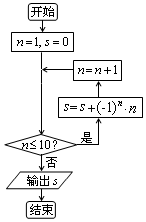

| A. | -6 | B. | 6 | C. | -5 | D. | 5 |