题目内容
设等差数列{an}的前n项和为Sn,公差为d.已知S2,S3+1,S4成等差数列.
(Ⅰ)求d的值;
(Ⅱ)若a1,a2,a5成等比数列,求
(n∈N*)的最大值.
(Ⅰ)求d的值;
(Ⅱ)若a1,a2,a5成等比数列,求
| an-2 |
| Sn |
考点:数列的求和
专题:计算题,等差数列与等比数列
分析:(Ⅰ)由S2,S3+1,S4成等差数列,得S2+S4=2(S3+1),利用等差数列求和公式可化为a1和d的方程,解出可得d;
(Ⅱ)由a1,a2,a5成等比数列,得a22=a1a5,可求得a1,从而可得an和Sn,借助二次函数性质可求
的最大值;
(Ⅱ)由a1,a2,a5成等比数列,得a22=a1a5,可求得a1,从而可得an和Sn,借助二次函数性质可求
| an-2 |
| Sn |
解答:
解:(Ⅰ)由S2,S3+1,S4成等差数列,
得S2+S4=2(S3+1),即(2a1+d)+(4a1+6d)=2(3a1+3d)+2,
解得d=2.
(Ⅱ)由a1,a2,a5成等比数列,得a22=a1a5,即(a1+d)2=a1(a1+4d),
解得a1=1.
∴an=a1+(n-1)d=2n-1,Sn=
=n2.
∴
=
=-3(
-
)2+
.
∴当n=3时,
的最大值为
.
得S2+S4=2(S3+1),即(2a1+d)+(4a1+6d)=2(3a1+3d)+2,
解得d=2.
(Ⅱ)由a1,a2,a5成等比数列,得a22=a1a5,即(a1+d)2=a1(a1+4d),
解得a1=1.
∴an=a1+(n-1)d=2n-1,Sn=
| n(a1+an) |
| 2 |
∴
| an-2 |
| Sn |
| 2n-3 |
| n2 |
| 1 |
| n |
| 1 |
| 3 |
| 1 |
| 3 |
∴当n=3时,
| an-2 |
| Sn |
| 1 |
| 3 |
点评:本题考查等差数列、等比数列的通项公式求和公式、二次函数的性质,考查学生的运算求解能力,属基础题.

练习册系列答案
相关题目
若正实数x,y满足x+y=2,且
≥M恒成立,则M的最大值为( )
| 1 |
| xy |
| A、1 | B、2 | C、3 | D、4 |
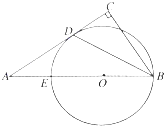 如图,在Rt△ABC中,∠C=90°,E为AB上一点,以BE为直径作圆O与AC相切于点D.若AB:BC=2:1,CD=
如图,在Rt△ABC中,∠C=90°,E为AB上一点,以BE为直径作圆O与AC相切于点D.若AB:BC=2:1,CD= 某居民1999~2003年货币收入x与购买商品支出Y的统计资料如表所示,单位:亿元
某居民1999~2003年货币收入x与购买商品支出Y的统计资料如表所示,单位:亿元