Question

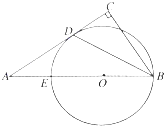如图，在Rt△ABC中，∠C=90°，E为AB上一点，以BE为直径作圆O与AC相切于点D．若AB：BC=2：1，CD=

3

，则圆O的半径长为

 

．

Answer 1

考点：与圆有关的比例线段

专题：选作题,立体几何

分析：连接DE，由直径所对的圆周角为直角可得∠BDE=∠C=90°，又AC切圆O于点D，根据弦切角定理可得∠BED=∠BDC，又由AB：BC=2：1，∴∠A=30°，从而∠ABC=60°，于是∠EBD=∠CBD=

1

2

∠ABC=30°，而CD=

3

，可得BD，进而在Rt△BED中即可得出．

解答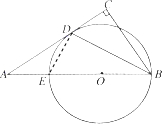： 解：连接DE，则∠BDE=∠C=90°，
由AB：BC=2：1，∴∠A=30°，从而∠ABC=60°，
又∵AC切圆O于点D，故∠BED=∠BDC，
从而：∠EBD=∠CBD=

1

2

∠ABC=30°，
而CD=

3

，
∴BD=2CD=2

3

，
∴BE=

BD

cos30°

=4．
故圆O的半径：r=

1

2

BE=2．
故答案为：2

点评：熟练掌握圆的性质、弦切角定理、含30°角的直角三角形的性质是解题的关键．