Question

有一块半径为R，圆心角为60°（∠AOB=60°）的扇形木板，已知扇形内有一内接矩形，求内接矩形面积最大值为多少？

Answer 1

考点：扇形面积公式

专题：计算题,应用题

分析：如图先用所给的角将矩形的面积表示出来，建立三角函数模型，再根据所建立的模型利用三角函数的性质求最值．

解答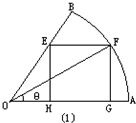： 解：内接矩形的放置有两种情况，如图（1）设∠FOA=θ，则FG=Rsinθ，
在△OEF中，EF=

2Rsin(60°-θ)

3

．
又设矩形EFGH的面积为S，那么S=FG•EF=

2R2sin(60°-θ)sinθ

3

=

R2

3

[cos（2θ-60°）-

1

2

]，
又∵0°＜θ＜60°，故当cos（2θ-60°）=1，即θ=30°时，S取最大值

R2

3

（1-

1

2

）=

3 R2

6

，
如图（2），设∠FOA=θ，则EF=2Rsin（30°-θ），在△OFG中，∠OGF=150°，
故

FG

sinθ

=

R

sin150°

即FG=2Rsinθ
设矩形的面积为S．
那么S=EFFG=4R²sinθsin（30°-θ）
=2R²[cos（2θ-30°）-cos30°]
=2R2[cos（2θ-30°）-

3

2

]
又∵0＜θ＜30°，故当cos（2θ-30°）=1即θ=15°时，S取最大值R2（2-

3

），
显然

3

6

R²＞（2-

3

）R²，
所以内接矩形的最大面积为

3

6

R²．

点评：本题关键是如何利用角θ表示矩形的长与宽，合理地把长与宽放在三角形中，利用正弦定理或三角定义来表示，本题属于中档题．