题目内容
把底面半径为8的圆锥放倒在平面内，使圆锥在此平面内绕圆锥顶点S滚动，当这个圆锥在平面内转回到原位置时，圆锥本身滚动了2周，则圆锥的母线长为 ，体积为 ．
考点：旋转体（圆柱、圆锥、圆台）
专题：空间位置关系与距离
分析：由已知可得圆锥展开图的圆心角为180°，结合圆锥的底面半径为8，和
=
（其中n为圆锥侧面展开图的圆心角），可得圆锥的母线长，进而求出圆锥的高后，代入圆锥的体积公式，可得答案．
| r |
| l |
| n° |
| 360° |
解答：
解：∵圆锥在平面内转回到原位置时，圆锥本身滚动了2周，
故圆锥展开图的圆心角为180°，
故圆锥的母线l满足：
=
，
∵r=8，
∴l=16，
故圆锥的高h=
=8
，
故圆锥的体积V=
πr2h=
π，
故答案为：16，
π
故圆锥展开图的圆心角为180°，
故圆锥的母线l满足：
| r |
| l |
| 1 |
| 2 |
∵r=8，
∴l=16，
故圆锥的高h=
| l2-r2 |
| 3 |
故圆锥的体积V=
| 1 |
| 3 |
| 512 |
| 3 |
| 3 |
故答案为：16，
| 512 |
| 3 |
| 3 |
点评：本题考查的知识点是旋转体，熟练掌握圆锥半径，母线，侧面展开图圆心角，圆锥的高之间的关系，是解答的关键．
练习册系列答案
阅读快车系列答案
相关题目
设集合M={1，2，3，4}，集合N={3，4，6}，全集U={1，2，3，4，5，6}，则集合M∩（∁UN）=（ ）
| A、{1} |
| B、{1，2} |
| C、{3，4} |
| D、{1，2，4，5} |
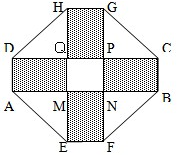某小区要建一座八边形的休闲公园，它的主体造型的平面图是由两个相同的举行ABCD和EFGH构成的面积为200m2的十字型地域，计划在正方形MNPQ上建一座花坛，造价为4200元/m2，在四个相同的矩形上（途中阴影部分）铺花岗岩地坪，造价为210元/m2，再在四个角上铺草坪，造价为80元/m2．受地域影响，AD的长最多能达到2已知点P是抛物线y2=4x上一点，设点P到此抛物线的准线的距离为d1，到直线x+2y-12=0的距离为d2，则d1+d2的最小值是（ ）
| A、5 | ||||
| B、4 | ||||
C、
| ||||
D、
|