题目内容
已知函数f(x)=lg(x2+ax+1)
(1)若f(x)定义域为R,求实数a的取值范围;
(2)若函数f(x)值域为R,求实数a的取值范围;
(3)若函数f(x)值域为[-2,+∞),求实数a的值;
(4)若函数f(x)在区间(-∞,2]上单调递减,求实数a的取值范围.
(1)若f(x)定义域为R,求实数a的取值范围;
(2)若函数f(x)值域为R,求实数a的取值范围;
(3)若函数f(x)值域为[-2,+∞),求实数a的值;
(4)若函数f(x)在区间(-∞,2]上单调递减,求实数a的取值范围.
考点:对数函数的图像与性质
专题:函数的性质及应用
分析:(1)只需判别式小于0即可;
(2)只需真数取遍所有正数即可;
(3)值域为[-2,+∞),说明-2是函数值,依此可得真数的最小值,进一步列出方程求a;
(4)一是考虑原式有意义,二是考虑对称轴与2的关系.
(2)只需真数取遍所有正数即可;
(3)值域为[-2,+∞),说明-2是函数值,依此可得真数的最小值,进一步列出方程求a;
(4)一是考虑原式有意义,二是考虑对称轴与2的关系.
解答:
解:(1)要使定义域为R,只需x2+ax+1>0恒成立,所以判别式a2-4<0,解得-2<a<2;
(2)要使值域为R,只需真数x2+ax+1取遍所有正实数,则应有a2-4≥0,解得a≥2或a≤-2.
(3)令t=x2+ax+1=(x+
)2+1-
,因为原函数的值域为[-2,+∞),所以lg(1-
)=-2,即1-
=10-2,解得a=±
.
(4)由题意,要使原函数在(-∞,2]上递减,只需函数t=x2+ax+1在(-∞,2]上递减,且t(2)>0,
即
,无解.
(2)要使值域为R,只需真数x2+ax+1取遍所有正实数,则应有a2-4≥0,解得a≥2或a≤-2.
(3)令t=x2+ax+1=(x+
| a |
| 2 |
| a2 |
| 4 |
| a2 |
| 4 |
| a2 |
| 4 |
3
| ||
| 5 |
(4)由题意,要使原函数在(-∞,2]上递减,只需函数t=x2+ax+1在(-∞,2]上递减,且t(2)>0,
即
|
点评:本题考查复合函数的定义域、值域、单调性的求法,涉及到不等式恒成立的问题.属于基础题,难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知点P是抛物线y2=4x上一点,设点P到此抛物线的准线的距离为d1,到直线x+2y-12=0的距离为d2,则d1+d2的最小值是( )
| A、5 | ||||
| B、4 | ||||
C、
| ||||
D、
|
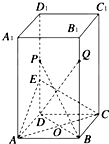 如图所示,已知正四棱柱ABCD-A1B1C1D1,点P为棱D1D的中点,且∠EOD=45°,AA1=2a,AB=a.
如图所示,已知正四棱柱ABCD-A1B1C1D1,点P为棱D1D的中点,且∠EOD=45°,AA1=2a,AB=a.