题目内容
已知盒中有n个黑球和m个白球,连续不放回地从中随机取球,每次取一个,直至盒中无球,规定:第i次取球若取到黑球得2i,取到白球不得分,记随机变量ξ为总的得分数.
(Ⅰ)当n=m=2时,求P(ξ=10);
(Ⅱ)若m=1,求随机变量ξ的期望E(ξ).
(Ⅰ)当n=m=2时,求P(ξ=10);
(Ⅱ)若m=1,求随机变量ξ的期望E(ξ).
考点:离散型随机变量的期望与方差
专题:综合题,概率与统计
分析:(Ⅰ)当n=m=2时,ξ=10表示4次中,第1次和第3次取到黑球,即可求出概率;
(Ⅱ)当m=1时,随机变量ξ的取值有:21+22+…+2n+1-2k,k=1,2,3,…,n+1,因为随机变量ξ的取值的概率为
,即可求随机变量ξ的期望E(ξ).
(Ⅱ)当m=1时,随机变量ξ的取值有:21+22+…+2n+1-2k,k=1,2,3,…,n+1,因为随机变量ξ的取值的概率为
| 1 |
| n+1 |
解答:
解:(Ⅰ)当n=m=2时,ξ=10表示4次中,第1次和第3次取到黑球,
所以P(ξ=10)=
=
;
(Ⅱ)当m=1时,随机变量ξ的取值有:21+22+…+2n+1-2k,k=1,2,3,…,n+1,
即2n+2-2-2k,k=1,2,3,…,n+1,
因为随机变量ξ的取值的概率为
,
所以期望E(ξ)=
[(2n+2-2-2)+…+(2n+2-2-2n+1)]=
.
所以P(ξ=10)=
| ||||
| 4! |
| 1 |
| 6 |
(Ⅱ)当m=1时,随机变量ξ的取值有:21+22+…+2n+1-2k,k=1,2,3,…,n+1,
即2n+2-2-2k,k=1,2,3,…,n+1,
因为随机变量ξ的取值的概率为
| 1 |
| n+1 |
所以期望E(ξ)=
| 1 |
| n+1 |
| n(2n+2-2) |
| n+1 |
点评:本题考查概率的计算,考查随机变量ξ的期望E(ξ),考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一简单组合体的三视图如图所示,则该组合体的体积为( )


| A、16-π | B、12-4π |
| C、12-2π | D、12-π |
某几何体的三视图如图所示(单位:cm),则该几何体的体积是( )
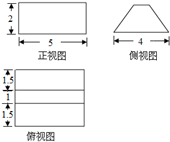

A、
| ||
| B、50cm3 | ||
C、
| ||
| D、25cm3 |
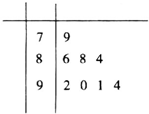 某校对高一年级8个班参加合唱比赛的得分进行了统计,得到样本的茎叶图(如图所示),则该样本的中位数和平均数分别是
某校对高一年级8个班参加合唱比赛的得分进行了统计,得到样本的茎叶图(如图所示),则该样本的中位数和平均数分别是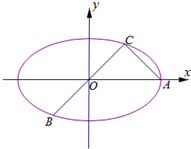 如图所示,已知A、B、C是长轴长为4的椭圆E上的三点,点A是长轴的一个端点,BC过椭圆中心O,且
如图所示,已知A、B、C是长轴长为4的椭圆E上的三点,点A是长轴的一个端点,BC过椭圆中心O,且