题目内容

在1个单位长度的线段AB上任取一点P，则点P到A、B两点的距离都不小于
1
6
的概率为
 
．
考点：几何概型
专题：概率与统计
分析：由题意可得，属于与区间长度有关的几何概率模型，试验的全部区域长度为1，基本事件的区域长度为
2
3
，代入几何概率公式可求．
解答： 解：设“1个单位长度的线段AB”对应区间长度为1，
“与线段两端点A、B的距离均不小于
1
6
”为事件 A，则满足A的区间长度为1-2×
1
6
=
2
3

根据几何概率的计算公式可得，P（A）=
2
3
1
=
2
3
．
故答案为：
2
3
点评：本题主要考查了几何概型，解答的关键是将原问题转化为几何概型问题后应用几何概率的计算公式求解．
练习册系列答案
相关题目
直线l与双曲线
x2
2
-y2=1的同一支相交于A，B两点，线段AB的中点在直线y=2x上，则直线AB的斜率为（　　）
A、4
B、2
C、
1
2
D、
1
4
已知盒中有n个黑球和m个白球，连续不放回地从中随机取球，每次取一个，直至盒中无球，规定：第i次取球若取到黑球得2i，取到白球不得分，记随机变量ξ为总的得分数．
（Ⅰ）当n=m=2时，求P（ξ=10）；
（Ⅱ）若m=1，求随机变量ξ的期望E（ξ）．
有以下命题：
①一个简谐运动的函数表达式为f(x)=sin(
1
2
x+
3π
4
)，则这个简谐运动的函数的最小正周期为4π；
②已知函数f（x）=loga(x-
87
2
)+89，(a＞0且a≠1)恒过定点（m，n），则m，n使等式m=sin21°+sin22°+sin23°+…+sin2n°成立；
③对于函数f（x）=x2+ax+b和g(x)=logax(0＜a＜1)，有f(
x1+x2
2
)≤f(x1)+f(x2)和g(
x1+x2
2
)≥g(x1)+g(x2)成立；
④定义：若任意x∈A，总有a-x∈A，（A≠∅），就称集合A为a的闭集．已知集合A⊆{1，2，3，4，5，6}，且A为6的闭集，则这样的集合A共有7个；
其中所有正确叙述的命题序号是
 
．
已知椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的右焦点为F，过F作斜率为
b
a
的直线与椭圆交于A，B两点，若|FB|≥2|FA|，则椭圆的离心率e的取值范围是
 
．
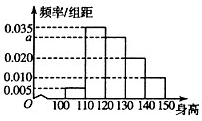从某小学随机抽取100名同学，将他们的身高（单位：厘米）数据绘制成频率分布直方图（如图）．若要从身高在[120，130），[130，140），[l40，150]三组内的学生中，用分层抽样的方法选取30人参加一项活动，则从身高在[120，130）的学生中选取的人数应为
 
．
若F1、F2是双曲线
x2
4
-
y2
5
=1的两个焦点，点P是该双曲线上一点，满足|PF1|+|PF2|=9，则|PF1|•|PF2|=（　　）
A、4
B、5
C、
65
4
D、2
cos
π
9
•cos
2π
9
•cos（-
23π
9
）=（　　）
A、-
1
8
B、-
1
16
C、
1
16
D、
1
8
已知关于x，y的方程C：x2+y2-2x-4y+m=0，m∈R．
（Ⅰ）若方程C表示圆，求m的取值范围；
（Ⅱ）若圆C与直线l：4x-3y+7=0相交于M，N两点，且|MN|=2
3
，求m的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网